
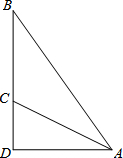
 如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高度为5m.
如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高度为5m. 分析 设CD=x,则AD=2x,根据勾股定理求出AC的长,从而求出CD、AC的长,然后根据勾股定理求出BD的长,即可求出BC的长.
解答 解:设CD=x,则AD=2x,
由勾股定理可得,AC=$\sqrt{{x}^{2}+(2x)^{2}}$=$\sqrt{5}$x,
∵AC=3$\sqrt{5}$米,
∴$\sqrt{5}$x=3$\sqrt{5}$,
∴x=3(米),
∴CD=3米,
∴AD=2×3=6米,
在Rt△ABD中,BD=$\sqrt{1{0}^{2}-{6}^{2}}$=8(米),
∴BC=8-3=5(米).
故答案为:5米.
点评 本题考查了解直角三角形的应用--坡度坡角问题,找到合适的直角三角形,熟练运用勾股定理是解题的关键.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
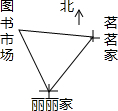 周末茗茗、丽丽两人相约去图书市场,8时丽丽开始从家以2千米/小时的速度沿北偏西25°的方向步行,9时茗茗开始从自己家以4千米/小时的速度沿一定的方向骑行,10时她们同时到达图书市场,如图所示,已知茗茗、丽丽两家相距4千米,则茗茗家与丽丽家的相对位置是( )
周末茗茗、丽丽两人相约去图书市场,8时丽丽开始从家以2千米/小时的速度沿北偏西25°的方向步行,9时茗茗开始从自己家以4千米/小时的速度沿一定的方向骑行,10时她们同时到达图书市场,如图所示,已知茗茗、丽丽两家相距4千米,则茗茗家与丽丽家的相对位置是( )| A. | 茗茗家在丽丽家北偏西55°方向 | B. | 茗茗家在丽丽家北偏东55°方向 | ||
| C. | 茗茗家在丽丽家南偏西35°方向 | D. | 茗茗家在丽丽家北偏东35°方向 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
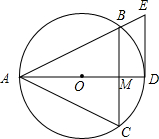 已知等边△ABC内接于⊙O,AD为O的直径交线段BC于点M,DE∥BC,交AB的延长线于点E.
已知等边△ABC内接于⊙O,AD为O的直径交线段BC于点M,DE∥BC,交AB的延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
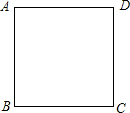 在数学课上,张老师设计了一个游戏,让电动娃娃在边长为1的正方形的四个顶点上依次跳动.规定:从顶点A出发,每跳动一步的长均为1.第一次顺时针方向跳1步到达顶点D,第二次逆时针方向跳2步到达顶点B,第三次顺时针方向跳3步到达顶点C,第四次逆时针方向跳4步到达顶点C,…,以此类推,跳动第2014次到达的顶点是( )
在数学课上,张老师设计了一个游戏,让电动娃娃在边长为1的正方形的四个顶点上依次跳动.规定:从顶点A出发,每跳动一步的长均为1.第一次顺时针方向跳1步到达顶点D,第二次逆时针方向跳2步到达顶点B,第三次顺时针方向跳3步到达顶点C,第四次逆时针方向跳4步到达顶点C,…,以此类推,跳动第2014次到达的顶点是( )| A. | A | B. | B | C. | C | D. | D |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com