
分析 (1)仿照已知等式得到一般性规律,写出即可;
(2)根据得出的规律确定出a与b的值,即可求出a+b的值;
(3)根据题意写出满足题意的等式,验证即可.
解答 解:(1)根据题意得:$\sqrt{n}$+$\frac{\sqrt{n}}{n-1}$=$\frac{n\sqrt{n}}{n-1}$(n≥3的整数);
(2)根据题意得:$\sqrt{10}$+$\frac{\sqrt{10}}{9}$=$\frac{10\sqrt{10}}{9}$,得到a=$\sqrt{10}$,b=9,即a+b=$\sqrt{10}$+9;
(3)$\sqrt{11}$+$\frac{\sqrt{11}}{10}$=$\frac{11\sqrt{11}}{10}$.
故答案为:(1)$\sqrt{n}$+$\frac{\sqrt{n}}{n-1}$=$\frac{n\sqrt{n}}{n-1}$(n≥3的整数);(2)$\sqrt{10}$+9
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:选择题
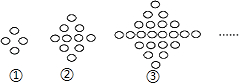 如图,第①个图形中有4个“○”,第②个图形中有10个“○”,第③个图形中有22个“○”,…,那么第⑤个图形中“○”的个数是( )
如图,第①个图形中有4个“○”,第②个图形中有10个“○”,第③个图形中有22个“○”,…,那么第⑤个图形中“○”的个数是( )| A. | 190 | B. | 94 | C. | 70 | D. | 46 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
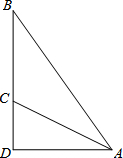 如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高度为5m.
如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高度为5m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
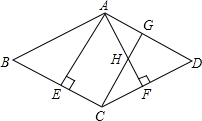 如图所示,菱形ABCD中,AB=4,E为BC中点,AE⊥BC,AF⊥CD,CG∥AE,CG交AF于点H,交AD于点G.
如图所示,菱形ABCD中,AB=4,E为BC中点,AE⊥BC,AF⊥CD,CG∥AE,CG交AF于点H,交AD于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com