练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．计算：${（{\frac{1}{3}}）^{-1}}-\root{3}{8}+\sqrt{2}×\frac{1}{{\sqrt{2}-1}}+{（-1）^{2015}}$．

    分析 直接利用负指数幂的性质以及立方根的性质、二次根式的乘法分别化简各数求出答案．

    解答 解：原式=3-2+$\frac{\sqrt{2}（\sqrt{2}+1）}{（\sqrt{2}-1）（\sqrt{2}+1）}$-1
    =2+$\sqrt{2}$．

    点评 此题主要考查了二次根式的化简、负整数指数幂的性质、立方根的性质等知识，正确化简各数是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    8．如图，已知矩形ABCD中，AB=2，在BC上取一点E，沿AE将△ABE向上折叠，使B点落在AD上的F点处，若四边形EFDC与矩形ABCD相似，则AD=（　　）
    A．$\sqrt{5}$B．$\sqrt{5}+1$C．4D．$2\sqrt{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．如果代数式3x-2与$\frac{1}{2}$互为倒数，那么x的值为$\frac{4}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

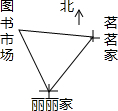    6．周末茗茗、丽丽两人相约去图书市场，8时丽丽开始从家以2千米/小时的速度沿北偏西25°的方向步行，9时茗茗开始从自己家以4千米/小时的速度沿一定的方向骑行，10时她们同时到达图书市场，如图所示，已知茗茗、丽丽两家相距4千米，则茗茗家与丽丽家的相对位置是（　　）
    A．茗茗家在丽丽家北偏西55°方向B．茗茗家在丽丽家北偏东55°方向
    C．茗茗家在丽丽家南偏西35°方向D．茗茗家在丽丽家北偏东35°方向

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．一次函数$y=\frac{x}{2}-1$在y轴上的截距为-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．观察等式：$\sqrt{3}+\frac{{\sqrt{3}}}{2}=\frac{{3\sqrt{3}}}{2}，2+\frac{2}{3}=\frac{4×2}{3}，\sqrt{5}+\frac{{\sqrt{5}}}{4}=\frac{{5\sqrt{5}}}{4}$，…
    （1）你能猜想有什么规律呢？请用含n的式子表示（n≥3的整数）$\sqrt{n}$+$\frac{\sqrt{n}}{n-1}$=$\frac{n\sqrt{n}}{n-1}$（n≥3的整数）；
    （2）按上述规律，若$\sqrt{10}+\frac{a}{b}=\frac{10a}{9}$，则a+b=$\sqrt{10}$+9；
    （3）仿照上面内容，另编一个等式，验证你在（1）中得到的规律．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．先化简$\frac{{{x^2}-1}}{{{x^2}-x-2}}÷（\frac{3}{2-x}-x-2）$，再从-2，-1，0，1四个数中选取一个适当的数作为x的值代入求值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．如图，在平面直角坐标系xOy中，矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上，反比例函数y=$\frac{k}{x}$（x＞0）与AB相交于点D，与BC相交于点E，若BE=4EC，且△ODE的面积是5，则k的值为$\frac{25}{12}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．等边三角形的边长为3，则该三角形的面积为$\frac{9\sqrt{3}}{4}$．

    查看答案和解析>>

    同步练习册答案