练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
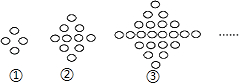
    13．如图，第①个图形中有4个“○”，第②个图形中有10个“○”，第③个图形中有22个“○”，…，那么第⑤个图形中“○”的个数是（　　）
    A．190B．94C．70D．46

    分析 由图可知：第①个图形中有1+2+1=4个“○”，第②个图形中有1+2+4+2+1=10个“○”，第③个图形中有1+2+4+8+4+2+1=22个“○”，…，得出第n个图形中有1+2+22+23+…+2n…+23+22+2+1个“○”，由此规律求得答案即可．

    解答 解：∵第①个图形中有1+2+1=4个“○”，
    第②个图形中有1+2+4+2+1=10个“○”，
    第③个图形中有1+2+4+8+4+2+1=22个“○”，
    …，
    ∴第⑤个图形中“○”的个数是1+2+4+8+16+32+16+8+4+2+1=94．
    故选：B．

    点评 此题考查图形的变化规律，找出图形之间的联系，得出数字之间的运算规律，利用规律解决问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    3．甲数比乙数的$\frac{1}{4}$还多1，设乙数为x，则甲数可表示为（　　）
    A．$\frac{1}{4}x+1$B．4x-1C．4（x-1）D．4（x+1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．计算
    （1）-14-$\sqrt{16}÷{（{-\frac{1}{2}}）^2}+{|{-3}|^3}$
    （2）6tan230°-cos30°•tan60°-2sin45°+cos60°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．化简下列各式：
    （1）4（a+b）2-2（a+b）（2a-2b）
    （2）$-（m+2）÷（m-1+\frac{2m+1}{m+1}）-\frac{1}{m}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．如图，已知矩形ABCD中，AB=2，在BC上取一点E，沿AE将△ABE向上折叠，使B点落在AD上的F点处，若四边形EFDC与矩形ABCD相似，则AD=（　　）
    A．$\sqrt{5}$B．$\sqrt{5}+1$C．4D．$2\sqrt{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．已知am=2，an=3．
    （1）填空：a2m=4，a3m•a（2n）=72
    （2）计算am-2n．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．方程组$\left\{\begin{array}{l}-x+y=3\\-x-y=1\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．计算（$\frac{1}{2}$）2014•22014的结果是（　　）
    A．0B．1C．-1D．24028

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．观察等式：$\sqrt{3}+\frac{{\sqrt{3}}}{2}=\frac{{3\sqrt{3}}}{2}，2+\frac{2}{3}=\frac{4×2}{3}，\sqrt{5}+\frac{{\sqrt{5}}}{4}=\frac{{5\sqrt{5}}}{4}$，…
    （1）你能猜想有什么规律呢？请用含n的式子表示（n≥3的整数）$\sqrt{n}$+$\frac{\sqrt{n}}{n-1}$=$\frac{n\sqrt{n}}{n-1}$（n≥3的整数）；
    （2）按上述规律，若$\sqrt{10}+\frac{a}{b}=\frac{10a}{9}$，则a+b=$\sqrt{10}$+9；
    （3）仿照上面内容，另编一个等式，验证你在（1）中得到的规律．

    查看答案和解析>>

    同步练习册答案