
【题目】某水晶厂生产的水晶工艺品非常畅销,某网店专门销售这种工艺品.成本为30元/件,每天销售y(件)与销售单价x(元)之间存在一次函数关系,当x=40时,y=300;当x=55时,y=150.
(1)求y与x之间的函数关系式;
(2)如果规定每天工艺品的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该工艺品销售单价的范围.
【答案】(1)![]() ;(2)当销售单价为46元时,每天获取的利润最大,最大利润是3840元;(3)当45≤x≤55时,捐款后每天剩余利润不低于3600元.
;(2)当销售单价为46元时,每天获取的利润最大,最大利润是3840元;(3)当45≤x≤55时,捐款后每天剩余利润不低于3600元.
【解析】
(1)根据每天销售y(件)与销售单价x(元)之间存在一次函数关系,用待定系数法将![]() ,
,![]() ,
,![]() ,
,![]() 代入
代入![]() 中可求出
中可求出![]() 和
和![]() 的值,即可得到
的值,即可得到![]() 与
与![]() 之间的函数关系式;(2)设利润为
之间的函数关系式;(2)设利润为![]() 元,根据每天工艺品的销售量不低于240件求出
元,根据每天工艺品的销售量不低于240件求出![]() 的范围,再根据总利润=单件利润
的范围,再根据总利润=单件利润![]() 销售量得出
销售量得出![]() 与
与![]() 之间的函数关系式,根据二次函数的性质求出最值.(3)根据每天捐出150元后每天剩余利润等于3600元列一元二次方程,根据二次函数的图像,求出
之间的函数关系式,根据二次函数的性质求出最值.(3)根据每天捐出150元后每天剩余利润等于3600元列一元二次方程,根据二次函数的图像,求出![]() 的范围,即所求销售单价的范围.
的范围,即所求销售单价的范围.
(1)设y与x之间的函数关系式:![]()
由题意得:![]() ,解得:
,解得:![]() ,
,
∴y与x之间的函数关系式为:![]() .
.
(2)设利润为![]() 元,
元,
由题意,得![]() ,解得
,解得![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]() 时,
时,![]() 随
随![]() 的增大而增大,
的增大而增大,
∴![]() 时,
时,![]() ,
,
答:当销售单价为46元时,每天获取的利润最大,最大利润是3840元.
(3)![]() ,
,
![]() ,
,
解得:![]() ,
,![]() ,
,
结合二次函数图象可得:
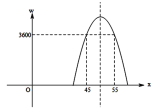
当![]() 时,捐款后每天剩余利润不低于3600元.
时,捐款后每天剩余利润不低于3600元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校将进行“校春季运动会”,现从全校学生中选出![]() 名同学参加运动会相关服务工作,其中
名同学参加运动会相关服务工作,其中![]() 名男生,
名男生,![]() 名女生.
名女生.
(1)若从这![]() 名同学中随机选取
名同学中随机选取![]() 人作为联络员,求选到男生的概率.
人作为联络员,求选到男生的概率.
(2)若运动会的某项服务工作只在![]() ,
,![]() 两位同学中选一人,准备用游戏的方式决定谁参加.游戏规则是:四个乒乓球上的数字分别为
两位同学中选一人,准备用游戏的方式决定谁参加.游戏规则是:四个乒乓球上的数字分别为![]() ,
,![]() ,
,![]() ,
,![]() (乒乓球只有数字不同,其余完全相同),将乒乓球放在不透明的纸箱中,从中任意摸取两个,若取到的两个乒乓球上的数字之和大于
(乒乓球只有数字不同,其余完全相同),将乒乓球放在不透明的纸箱中,从中任意摸取两个,若取到的两个乒乓球上的数字之和大于![]() 则选
则选![]() ,否则选
,否则选![]() ,从是否公平的角度看,该游戏规则是否合理,用树状图或表格说明理由.
,从是否公平的角度看,该游戏规则是否合理,用树状图或表格说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,点D在AB边上(不与点A、B重合),以CD为腰作等腰直角
,点D在AB边上(不与点A、B重合),以CD为腰作等腰直角![]() ,
,![]() .
.
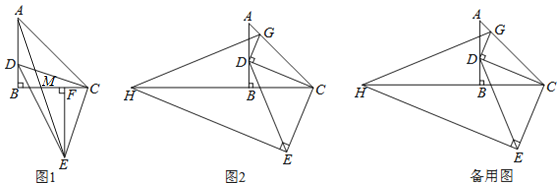
(1)如图1,作![]() 于F,求证:
于F,求证:![]() ;
;
(2)在图1中,连接AE交BC于M,求![]() 的值。
的值。
(3)如图2,过点E作![]() 交CB的延长线于点H,过点D作
交CB的延长线于点H,过点D作![]() ,交AC于点G,连接GH当点D在边AB上运动时,式子
,交AC于点G,连接GH当点D在边AB上运动时,式子![]() 的值会发生变化吗?若不变,求出该值:若变化请说明理由.
的值会发生变化吗?若不变,求出该值:若变化请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
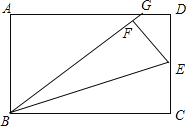
【题目】如图,在矩形ABCD中,点E是CD的中点,将△BCE沿BE折叠后得到△BEF、且点F在矩形ABCD的内部,将BF延长交AD于点G.若![]() ,则
,则![]() =__.
=__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】活跃校园气氛,增强班集体凝聚力,培养学生团结协作意识,重庆一中举行了秋季趣味运动会.赛后为了了解初二年级的学生们对新增比赛项目“毛毛虫赛跑”的喜欢程度(以下称:喜欢度),对该年级的学生进行了调查,被调查的学生对该比赛项目的喜欢度分别记为:5分、4分、3分、2分、1分(其中5分为超喜欢、4分为很喜欢、3分为喜欢、2分为一般、1分为不喜欢),并将调查结果绘制成如下两幅不完整的统计图:
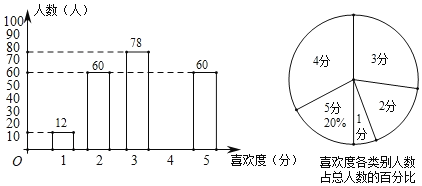
请你根据图中提供的信息,回答下列问题:
(1)被调查的学生总数是______人,并补全条形统计图;
(2)写出被调查学生喜欢度分数的中位数是______分,众数是______分;
(3)求这批被调查学生喜欢度分数的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线![]() :
:![]() 与直线
与直线![]() :
:![]() 交于点
交于点![]() ,已知点
,已知点![]() 的横坐标为-5,直线
的横坐标为-5,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
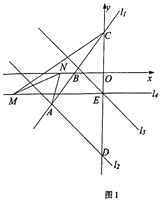
(1)求直线![]() 的解析式;
的解析式;
(2)将直线![]() 向上平移6个单位得到直线
向上平移6个单位得到直线![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,若点
,若点![]() 为垂线
为垂线![]() 上的一个动点,点
上的一个动点,点![]() 为
为![]() 轴上的一个动点,当
轴上的一个动点,当![]() 的值最小时,求此时点
的值最小时,求此时点![]() 的坐标及
的坐标及![]() 的最小值;
的最小值;
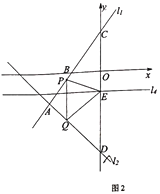
(3)已知点![]() 、
、![]() 分别是直线
分别是直线![]() 、
、![]() 上的两个动点,连接
上的两个动点,连接![]() 、
、![]() 、
、![]() ,是否存在点
,是否存在点![]() 、
、![]() ,使得
,使得![]() 是以点
是以点![]() 为直角顶点的等腰直角三角形,若存在,求点
为直角顶点的等腰直角三角形,若存在,求点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
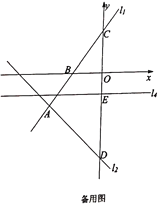
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.
设小明计划今年夏季游泳次数为x(x为正整数).
(I)根据题意,填写下表:
游泳次数 | 10 | 15 | 20 | … | x |
方式一的总费用(元) | 150 | 175 | ______ | … | ______ |
方式二的总费用(元) | 90 | 135 | ______ | … | ______ |
(Ⅱ)若小明计划今年夏季游泳的总费用为270元,选择哪种付费方式,他游泳的次数比较多?
(Ⅲ)当x>20时,小明选择哪种付费方式更合算?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意一个三位数![]() ,将它任意两个数位上的数字对调后得到一个首位不为0的新的三位数
,将它任意两个数位上的数字对调后得到一个首位不为0的新的三位数![]() (
(![]() 可以与
可以与![]() 相同),记
相同),记![]() ,在所有可能的情况中,当
,在所有可能的情况中,当![]() 最小时,我们称此时的
最小时,我们称此时的![]() 是
是![]() 的“平安快乐数”,并规定
的“平安快乐数”,并规定![]() .例如:318按上述方法可得新数381、813、138,因为
.例如:318按上述方法可得新数381、813、138,因为![]() ,
,![]() ,
,![]() ,而
,而![]() ,所以138是318的“平安快乐数”,此时
,所以138是318的“平安快乐数”,此时![]() .
.
(1)168的“平安快乐数”为_______________,![]() ______________;
______________;
(2)若![]() (
(![]() ,
,![]() 都是正整数),交换其十位与百位上的数字得到新数
都是正整数),交换其十位与百位上的数字得到新数![]() ,当
,当![]() 是13的倍数时,求
是13的倍数时,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县举办老、中、青三个年龄段五公里竞走活动,其人数比为![]() ,如图所示的扇形统计图表示 上述分布情况,已知老人有
,如图所示的扇形统计图表示 上述分布情况,已知老人有![]() 人,则下列说法不正确的是( )
人,则下列说法不正确的是( )
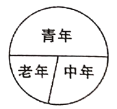
A. 老年所占区域的圆心角是![]() B. 参加活动的总人数是
B. 参加活动的总人数是![]() 人
人
C. 中年人比老年人多![]() D. 老年人比青年人少
D. 老年人比青年人少![]() 人
人
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com