
【题目】如图,四边形ABCD是边长为3的正方形,点E在边AD所在的直线上,连接CE,以CE为边,作正方形CEFG(点C、E、F、G按逆时针排列),连接BF.
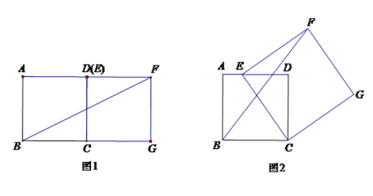
(1)如图1,当点E与点D重合时,BF的长为 ;
(2)如图2,当点E在线段AD上时,若AE=1,求BF的长;(提示:过点F作BC的垂线,交BC的延长线于点M,交AD的延长线于点N.)
(3)当点E在直线AD上时,若AE=4,请直接写出BF的长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)利用勾股定理即可求出.
(2)过点F作FH⊥AD交AD于的延长线于点H,作FM⊥AB于点M,证出![]() ,进而求得MF,BM的长,再利用勾股定理,即可求得.
,进而求得MF,BM的长,再利用勾股定理,即可求得.
(3)分两种情况讨论,同(2)证得三角形全等,再利用勾股定理即可求得.
(1)由勾股定理得:![]()
(2)过点F作FH⊥AD交AD于的延长线于点H,作FM⊥AB于点M,如图2所示:
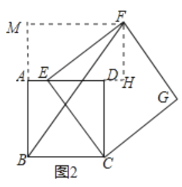
则FM=AH,AM=FH
∵四边形CEFG是正方形 ∴EC=EF,∠FEC=90° ∴∠DEC+∠FEH=90°,
又∵四边形![]() 是正方形 ∴∠ADC=90° ∴∠DEC+∠ECD=90°,∴∠ECD=∠FEH
是正方形 ∴∠ADC=90° ∴∠DEC+∠ECD=90°,∴∠ECD=∠FEH
又∵∠EDC=∠FHE=90°,∴![]() ∴FH=ED EH=CD=3
∴FH=ED EH=CD=3
∵AD=3,AE=1,ED=AD-AE=3-1=2,∴FH=ED=2
∴MF=AH=1+3=4,MB=FH+CD=2+3=5
在Rt△BFM中,BF=![]()
(3)分两种情况:
①当点E在边AD的左侧时,过点F作FM⊥BC交BC的反向延长线于点M,交DE于点N.如图3所示:
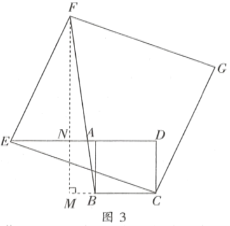
同(2)得:![]()
∴EN=CD=3,FN=ED=7
∵AE=4∴AN=AE-EN=4-3=1
∴MB=AN=1 FM=FN+NM=7+3=10
在![]() 中
中
由勾股定理得:![]()
②当点E在边AD的右侧时,过点F作FN⊥AD交AD的延长线于点N,交BC延长线于M,如图4所示:

同理得: ![]()
∴NF=DE=1,EN=CD=3
∴FM=3-1=2,CM=DN=DE+EN=1+3=4
∴BM=CB+CM=3+4=7
在![]() 中
中
由勾股定理得:![]()
故BF的长为![]()


科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队共同承担一项筑路任务,甲队单独施工完成此项任务比乙队单独施工完成此项任务多用10天,且甲队单独施工45天和乙队单独施工30天的工作量相同.
(1)甲、乙两队单独完成此项任务各需多少天?
(2)若甲、乙两队共同工作了3天后,乙队因设备检修停止施工,由甲队继续施工,为了不影响工程进度,甲队的工作效率提高到原来的2倍,要使甲队总的工作量不少于乙队的工作量的2倍,那么甲队至少再单独施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y1=x2-2x-3与x轴相交于点A,B(点A在B的左侧),与y轴相交于点C,直线y2=kx+b经过点B,C.
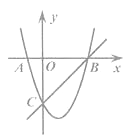
(1)求直线BC的函数关系式;
(2)当y1>y2时,请直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列问题:
![]() 画出数轴,并在数轴上表示
画出数轴,并在数轴上表示![]() 与
与![]() ;
;
![]() 数轴上表示
数轴上表示![]() 的点与表示
的点与表示![]() 的两点之间的距离为 ;
的两点之间的距离为 ;
![]() 若
若![]() ,且点
,且点![]() ,点
,点![]() 在数轴上表示的数分别是
在数轴上表示的数分别是![]() ,则
,则![]() 两点间的最大距离 ,最小距离是
两点间的最大距离 ,最小距离是
![]() 数轴上
数轴上![]() 的三点所表示的数分别为
的三点所表示的数分别为![]() .点
.点![]() 在点
在点![]() 左侧,点
左侧,点![]() 与点
与点![]() 之间的距离为
之间的距离为![]() ,点
,点![]() 与点
与点![]() 之间的距离为
之间的距离为![]() ,如果
,如果![]() 两点同时出发,点
两点同时出发,点![]() 以每分钟
以每分钟![]() 个单位长度的速度从点
个单位长度的速度从点![]() 向右运动,点
向右运动,点![]() 以每分钟
以每分钟![]() 个单位长度从点
个单位长度从点![]() 向左运动.
向左运动.
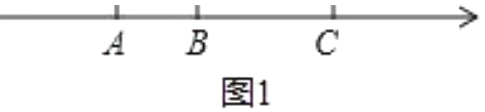
①如图1, 分钟后,点![]() 与点
与点![]() 的距离和点
的距离和点![]() 与点
与点![]() 的距离相等;
的距离相等;
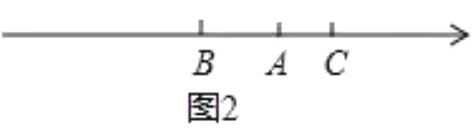
②如图2, 分钟后,点 ![]() 与点
与点![]() 的距离和点
的距离和点![]() 与点
与点![]() 的距离相等.
的距离相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为打造书香校园,计划购进甲乙两种规格的书柜放置新购置的图书,调查发现,若购买甲种书柜3个,乙种书柜2个,共需要资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个(其中乙种书柜的数量不少于甲种书柜的数量的![]() ).设该校计划购进甲种书柜m个,资金总额为W元.求W与m的函数关系式,并请你为该校设计资金最少的购买方案.
).设该校计划购进甲种书柜m个,资金总额为W元.求W与m的函数关系式,并请你为该校设计资金最少的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为调查达州市民上班时最常用的交通工具的情况,随机抽取了部分市民进行调查,要求被调查者从“A:自行车,B:电动车,C:公交车,D:家庭汽车,E:其他”五个选项中选择最常用的一项.将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题.
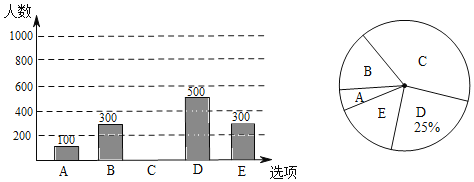
(1)本次调查中,一共调查了 名市民;扇形统计图中,B项对应的扇形圆心角是 度;补全条形统计图;
(2)若甲、乙两人上班时从A,B,C,D四种交通工具中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两人恰好选择同一种交通工具上班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某慈善组织租用甲、乙两种货车共![]() 辆,把蔬菜
辆,把蔬菜![]() 吨,水果
吨,水果![]() 吨,全部运到灾区已知辆甲种货车同时可装蔬菜
吨,全部运到灾区已知辆甲种货车同时可装蔬菜![]() 吨,水果
吨,水果![]() 吨;一辆乙种货车同时可装蔬菜
吨;一辆乙种货车同时可装蔬菜![]() 吨,水果
吨,水果![]() 吨.
吨.
(1)若将这批货物一次性运到灾区,请写出具体的租车方案?
(2)若甲种货车每辆需付燃油费![]() 元,乙种货车每辆需付燃油费
元,乙种货车每辆需付燃油费![]() 元,则应选(1)种的哪种方案,才能使所付的燃油费最少?最少的燃油费是多少元?
元,则应选(1)种的哪种方案,才能使所付的燃油费最少?最少的燃油费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
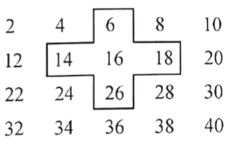
【题目】将连续的偶数2,4,6,8,…,排成如下表,并用一个十字形框架框住其中的五个数,请你仔细观察十字形框架中的数字的规律,并回答下列问题:
(1)十字框中的五个数的和等于 .
(2)若将十字框上下左右移动,可框住另外的五个数,设中间的数为![]() ,用代数式表示十字框中的五个数的和是 .
,用代数式表示十字框中的五个数的和是 .
(3)在移动十字框的过程中,若框住的五个数的和等于2020,这五个数从小到大依次是: , , , , ,……
(4)框住的五个数的和能等于2019吗?
答: (回答“能”或“不能”)
理由是:_______________________________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在第三象限的双曲线
在第三象限的双曲线![]() 上,过点
上,过点![]() 作
作![]() 轴交双曲线于点
轴交双曲线于点![]() ,连接
,连接![]() ,则
,则![]() 的面积为__________.
的面积为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com