
【题目】如图,已知反比例函数 ![]() 的图象经过点(
的图象经过点( ![]() ,8),直线y=﹣x+b经过该反比例函数图象上的点Q(4,m).
,8),直线y=﹣x+b经过该反比例函数图象上的点Q(4,m).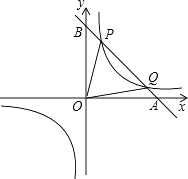
(1)求上述反比例函数和直线的函数表达式;
(2)设该直线与x轴、y轴分别相交于A、B两点,与反比例函数图象的另一个交点为P,连接0P、OQ,求△OPQ的面积.
【答案】
(1)
解:把点( ![]() ,8)代入反比例函数
,8)代入反比例函数 ![]() ,得k=
,得k= ![]() ×8=4,
×8=4,
∴反比例函数的解析式为y= ![]() ;
;
又∵点Q(4,m)在该反比例函数图象上,
∴4m=4,
解得m=1,即Q点的坐标为(4,1),
而直线y=﹣x+b经过点Q(4,1),
∴1=﹣4+b,
解得b=5,
∴直线的函数表达式为y=﹣x+5
(2)
解:联立 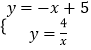 ,
,
解得 ![]() 或
或 ![]() ,
,
∴P点坐标为(1,4),
对于y=﹣x+5,令y=0,得x=5,
∴A点坐标为(5,0),
∴S△OPQ=S△AOB﹣S△OBP﹣S△OAQ
= ![]() ×5×5﹣
×5×5﹣ ![]() ×5×1﹣
×5×1﹣ ![]() ×5×1
×5×1
= ![]() .
.
【解析】(1)把点( ![]() ,8)代入反比例函数
,8)代入反比例函数 ![]() ,确定反比例函数的解析式为y=
,确定反比例函数的解析式为y= ![]() ;再把点Q(4,m)代入反比例函数的解析式得到Q的坐标,然后把Q的坐标代入直线y=﹣x+b,即可确定b的值;(2)把反比例函数和直线的解析式联立起来,解方程组得到P点坐标;对于y=﹣x+5,令y=0,求出A点坐标,然后根据S△OPQ=S△AOB﹣S△OBP﹣S△OAQ进行计算即可.
;再把点Q(4,m)代入反比例函数的解析式得到Q的坐标,然后把Q的坐标代入直线y=﹣x+b,即可确定b的值;(2)把反比例函数和直线的解析式联立起来,解方程组得到P点坐标;对于y=﹣x+5,令y=0,求出A点坐标,然后根据S△OPQ=S△AOB﹣S△OBP﹣S△OAQ进行计算即可.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC是等腰直角三角形,∠A=90°,D是腰AC上的一个动点,过C作CE垂直于BD或BD的延长线,垂足为E,如图. 
(1)若BD是AC的中线,求 ![]() 的值;
的值;
(2)若BD是∠ABC的角平分线,求 ![]() 的值;
的值;
(3)结合(1)、(2),试推断 ![]() 的取值范围(直接写出结论,不必证明),并探究
的取值范围(直接写出结论,不必证明),并探究 ![]() 的值能小于
的值能小于 ![]() 吗?若能,求出满足条件的D点的位置;若不能,说明理由.
吗?若能,求出满足条件的D点的位置;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.如表是该市居民“一户一表”生活用水及提示计费价格表的部分信息:(说明:①每户产生的污水量等于该户自来水用水量;②水费=自来水费用+污水处理费用)
已知小王家2012年4月份用水20吨,交水费66元;5月份用水25吨,交水费91元.
(1)求a、b的值;
(2)随着夏天的到来,用水量将增加.为了节省开支,小王计划把6月份的水费控制在不超过家庭月收入的2%.若小王家的月收入为9200元,则小王家6月份最多能用水多少吨?
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
17吨以下 | a | 0.80 |
超过17吨但不超过30吨部分 | b | 0.80 |
超过30吨的部分 | 6.00 | 0.80 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市今年的信息技术结业考试,采用学生抽签的方式决定自己的考试内容.规定:每位考生先在三个笔试题(题签分别用代码B1、B2、B3表示)中抽取一个,再在三个上机题(题签分别用代码J1、J2、J3表示)中抽取一个进行考试.小亮在看不到题签的情况下,分别从笔试题和上机题中随机地各抽取一个题签.
(1)用树状图或列表法表示出所有可能的结果;
(2)求小亮抽到的笔试题和上机题的题签代码的下标(例如“B1”的下表为“1”)均为奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列叙述正确的是( )
A. 符号不同的两个数是互为相反数
B. 一个有理数的相反数一定是负有理数
C. 2![]() 与2.75都是﹣
与2.75都是﹣![]() 的相反数
的相反数
D. 0没有相反数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K.过D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H. 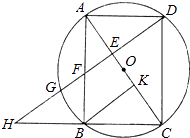
(1)求证:AE=CK;
(2)如果AB=a,AD= ![]() (a为大于零的常数),求BK的长:
(a为大于零的常数),求BK的长:
(3)若F是EG的中点,且DE=6,求⊙O的半径和GH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个长方形绿化带的长为(6a+4b)米,宽为(3a﹣2b)米.
(1)求该绿化带的面积(用含有a、b的代数式表示);
(2)当a=10,b=5时,该绿化带的面积是多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在长方形ABCD中,AB=DC=3cm,BC=5cm,点P从点B出发,以1 cm/s的速度沿BC向点C运动,设点P的运动时间为ts.
(1)PC= cm(用含t的代数式表示)
(2)当t为何值时,△ABP≌△DCP,请说明理由
(3)如图②,当点P从点B开始运动时,点Q从点C出发,以a cm/s的速度沿CD向点D运动,是否存在这样a的值,使得△ABP与△PCQ全等?若存在,请求出a的值,若不存在,请说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com