
【题目】已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K.过D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H. 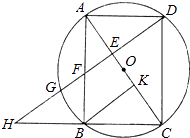
(1)求证:AE=CK;
(2)如果AB=a,AD= ![]() (a为大于零的常数),求BK的长:
(a为大于零的常数),求BK的长:
(3)若F是EG的中点,且DE=6,求⊙O的半径和GH的长.
【答案】
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∴∠DAE=∠BCK,
∵BK⊥AC,DH∥KB,
∴∠BKC=∠AED=90°,
∴△BKC≌△ADE,
∴AE=CK
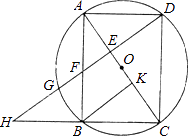
(2)解:∵AB=a,AD= ![]() =BC,
=BC,
∴AC= ![]() =
= ![]() =
= ![]()
![]()
∵BK⊥AC,∠ABC=90°,
∴在Rt△ABC中,由三角形的面积公式得: ![]() AB×BC=
AB×BC= ![]() AC×BK,
AC×BK,
∴a× ![]() a=
a= ![]() a×BK,
a×BK,
∴BK= ![]() a
a
(3)解:DG是圆的弦,又有AE⊥GD得GE=ED,
∵DE=6,
∴GE=6,
又∵F为EG中点,
∴EF= ![]() EG=3,
EG=3,
∵△BKC≌△DEA,
∴BK=DE=6,
∴EF= ![]() BK,且EF∥BK,
BK,且EF∥BK,
∴△AEF∽△AKB,且相似比为1:2,
∴EF为△ABK的中位线,
∴AF=BF,
又∵∠ADF=∠H,∠DAF=∠HBF=90°,
∴△AFD≌△BFH(AAS),
∴HF=DF=3+6=9,
∴GH=6,
∵DH∥KB,BK⊥AC,四边形ABCD为矩形,
∴∠AEF=∠DEA=90°,
∴∠FAE+∠DAE=∠FAE+∠AFE=90°,
∴∠AFE=∠DAE,
∴△AEF∽△DEA,
∴AE:ED=EF:AE,
∴AE2=EFED=3×6=18,
∴AE=3 ![]() ,
,
∵△AED∽△HEC,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴AE= ![]() AC,
AC,
∴AC=9 ![]() ,
,
则AO= ![]() ,
,
故⊙O的半径是 ![]() ,GH的长是6.
,GH的长是6.
【解析】(1)根据ABCD是矩形,求证△BKC≌△ADE即可;(2)根据勾股定理求得AC的长,根据三角形的面积公式得出 ![]() AB×BC=
AB×BC= ![]() AC×BK,代入即可求得BK.(3)根据三角形中位线定理可求出EF,再利用△AFD≌△HBF可求出HF,然后即可求出GH;利用射影定理求出AE,再利△AED∽△HEC求证AE=
AC×BK,代入即可求得BK.(3)根据三角形中位线定理可求出EF,再利用△AFD≌△HBF可求出HF,然后即可求出GH;利用射影定理求出AE,再利△AED∽△HEC求证AE= ![]() AC,然后即可求得AC即可.
AC,然后即可求得AC即可.
【考点精析】掌握三角形中位线定理和垂径定理是解答本题的根本,需要知道连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.顶点相对的两个角叫对顶角
B.一个角的补角大于这个角本身
C.互为补角的两个角不可能都是锐角
D.没有公共点的两条直线是平行线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
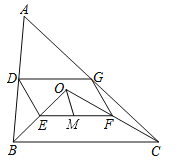
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数 ![]() 的图象经过点(
的图象经过点( ![]() ,8),直线y=﹣x+b经过该反比例函数图象上的点Q(4,m).
,8),直线y=﹣x+b经过该反比例函数图象上的点Q(4,m).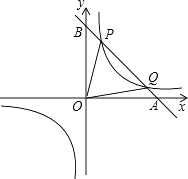
(1)求上述反比例函数和直线的函数表达式;
(2)设该直线与x轴、y轴分别相交于A、B两点,与反比例函数图象的另一个交点为P,连接0P、OQ,求△OPQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平行四边形ABCD中,CE平分∠BCD且交AD于点E,A F∥CE,且交BC于点F.
(1)求证:△ABF≌△CDE;
(2)如图,若∠1=65°,求∠B的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线CD与EF相交于点O,∠COE=60°,将一直角三角尺AOB的直角顶点与O重合,OA平分∠COE.
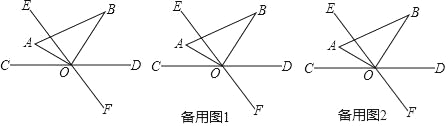
(1)求∠BOD的度数;
(2)将三角尺AOB以每秒3°的速度绕点O顺时针旋转,同时直线EF也以每秒9°的速度绕点O顺时针旋转,设运动时间为t秒(0≤t≤40).
①当t为何值时,直线EF平分∠AOB;
②若直线EF平分∠BOD,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,若要得到1000个小三角形,则需要操作的次数是( ) 
A.332
B.333
C.334
D.335
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com