
【题目】如图,直线CD与EF相交于点O,∠COE=60°,将一直角三角尺AOB的直角顶点与O重合,OA平分∠COE.
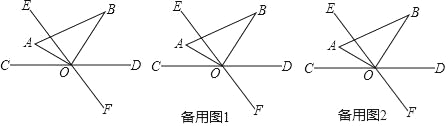
(1)求∠BOD的度数;
(2)将三角尺AOB以每秒3°的速度绕点O顺时针旋转,同时直线EF也以每秒9°的速度绕点O顺时针旋转,设运动时间为t秒(0≤t≤40).
①当t为何值时,直线EF平分∠AOB;
②若直线EF平分∠BOD,直接写出t的值.
【答案】(1)60°;(2)若直线EF平分∠BOD,t的值为12s或36s.
【解析】试题分析:(1)根据角平分线的性质,可得∠AOC的值,再根据互为补角和互为余角的性质,求出∠BOD的值;
(2)①根据题意,分为OE平分∠AOB和OF平分∠AOB两种情况讨论求解;
②根据题意,分两种情况:当OE平分∠BOD和OF平分∠BOD时,进行画图求解.
试题解析:(1)∵∠COE=60°,OA平分∠COE,
∴∠AOC=30°,
又∵∠AOB=90°,
∴∠BOD=180°﹣30°﹣90°=60°;
(2)①分两种情况:
当OE平分∠AOB时,∠AOE=45°,
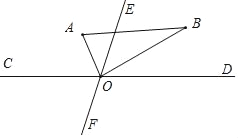
即9t+30°﹣3t=45°,
解得t=2.5;
当OF平分∠AOB时,AOF=45°,

即9t﹣150°﹣3t=45°,
解得t=32.5;
综上所述,当t=2.5s或32.5s时,直线EF平分∠AOB;
②t的值为12s或36s.
分两种情况:
当OE平分∠BOD时,∠BOE=![]() ∠BOD,
∠BOD,
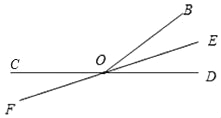
即9t﹣60°﹣3t=![]() (60°﹣3t),
(60°﹣3t),
解得t=12;
当OF平分∠BOD时,∠DOF=![]() ∠BOD,
∠BOD,
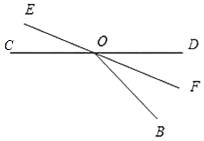
即3t﹣(9t﹣240°)=![]() (3t﹣60°),
(3t﹣60°),
解得t=36;
综上所述,若直线EF平分∠BOD,t的值为12s或36s.


科目:初中数学 来源: 题型:
【题目】已知△ABC是等腰直角三角形,∠A=90°,D是腰AC上的一个动点,过C作CE垂直于BD或BD的延长线,垂足为E,如图. 
(1)若BD是AC的中线,求 ![]() 的值;
的值;
(2)若BD是∠ABC的角平分线,求 ![]() 的值;
的值;
(3)结合(1)、(2),试推断 ![]() 的取值范围(直接写出结论,不必证明),并探究
的取值范围(直接写出结论,不必证明),并探究 ![]() 的值能小于
的值能小于 ![]() 吗?若能,求出满足条件的D点的位置;若不能,说明理由.
吗?若能,求出满足条件的D点的位置;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K.过D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H. 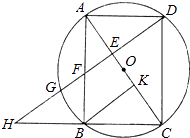
(1)求证:AE=CK;
(2)如果AB=a,AD= ![]() (a为大于零的常数),求BK的长:
(a为大于零的常数),求BK的长:
(3)若F是EG的中点,且DE=6,求⊙O的半径和GH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个长方形绿化带的长为(6a+4b)米,宽为(3a﹣2b)米.
(1)求该绿化带的面积(用含有a、b的代数式表示);
(2)当a=10,b=5时,该绿化带的面积是多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列一组图形,其中图形①中共有2颗星,图形②中共有6颗星,图形③中共有11颗星,图形④中共有17颗星,…,按此规律,图形⑧中星星的颗数是( ) 
A.43
B.45
C.51
D.53
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各为多少元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元.则有哪几种购车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在长方形ABCD中,AB=DC=3cm,BC=5cm,点P从点B出发,以1 cm/s的速度沿BC向点C运动,设点P的运动时间为ts.
(1)PC= cm(用含t的代数式表示)
(2)当t为何值时,△ABP≌△DCP,请说明理由
(3)如图②,当点P从点B开始运动时,点Q从点C出发,以a cm/s的速度沿CD向点D运动,是否存在这样a的值,使得△ABP与△PCQ全等?若存在,请求出a的值,若不存在,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位采购员同去一家饲料公司购买两次饲料.两次饲料的价格有变化,两位采购员的购货方式也不同,其中,甲每次购买1000千克,乙每次用去800元,而不管购买多少饲料.
(1)甲、乙所购饲料的平均单价各是多少?
(2)谁的购货方式更合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com