
【题目】在△ABC中,AB=AC,BC=12,E为边AC的中点,
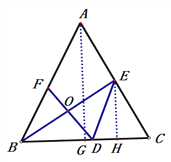
(1)如图1,过点E作EH⊥BC,垂足为点H,求线段CH的长;
(2)作线段BE的垂直平分线分别交边BC、BE、AB于点D、O、F.
①如图2,当∠BAC=90°时,求BD的长;
②如图3,设tan∠ACB=x,BD=y,求y与x之间的函数表达式和tan∠ACB的最大值.

【答案】(1)3(2)5(3)①![]() ②
②![]()
【解析】试题分析:(1)点A作AG⊥BC交BC于点G,则EH∥AG,由等腰三角形的性质得CG=6,再由E为AC中点可得H为CG的中点.
(2)①过点E作![]() 于点H,设
于点H,设![]() ,在Rt△EDH中可得
,在Rt△EDH中可得![]() ,解方程求出x的值;由
,解方程求出x的值;由![]()
![]() ,可得
,可得![]() ,
, ![]() ,在
,在![]() 中,根据勾股定理列出关系式
中,根据勾股定理列出关系式![]() ,然后整理可得y与x之间的函数表达式;求tan∠ACB的最大值有两种方法一是利用正切的增减性,二是利用数形结合.
,然后整理可得y与x之间的函数表达式;求tan∠ACB的最大值有两种方法一是利用正切的增减性,二是利用数形结合.
解:(1)点A作AG⊥BC交BC于点G.
∵![]() ,
,
∴![]() ,
,
∵E为AC中点,EH∥AG,
∴H为CG的中点,∴CH=3,
⑵①过点E作![]() 于点H,
于点H,
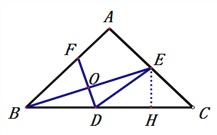
∵△ABC是等腰直角三角形,则CH=EH=3,
设![]() ,则
,则![]() ,
, ![]() ,
,
Rt△EDH中, ![]() ,
,
解之得, ![]() ,
,
即BD=5,
②∵![]()
![]() ,
,
∴![]() ,
, ![]() ,
,
在![]() 中,
中,
![]() ,
,
∴![]() ,
,
方法一:由![]() 得,
得, ![]() ,
,
当y有最大值时,x有最大值.即tan∠ACB有最大值.
∴当y=12时, ![]() ,
, ![]() (负的舍去),
(负的舍去),
∴tan∠ACB最大值为![]() ,
,
或方法二:当点D与点C重合时,tan∠ACB最大,
![]() ,
,
![]() .
.
BC边的高为![]() ,
,
此时tan∠ACB=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
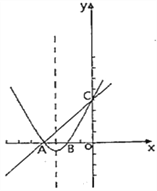
【题目】在平面直角坐标系xoy中,抛物线y=ax2+bx+c (a≠O)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点A的坐标为(-4,O),抛物线的对称轴是直线x=-3,且经过A、C两点的直线为y=kx+4.
(1)求抛物线的函数表达式;
(2)将直线AC向下平移m个单位长度后,得到的直线l与抛物线只有一个交点D,求m的值;
(3)抛物线上是否存在点Q,使点Q到直线AC的距离为![]() ?若存在,请直接写出Q的坐标,若不存在,请说明理由.
?若存在,请直接写出Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上 A、B 两点所对应的数分别是 a 和 b,且(a+5)2+|b﹣7|=0.
(1)求 a,b;A、B 两点之间的距离.
(2)有一动点 P 从点 A 出发第一次向左运动 1 个单位长度,然后在新的位置第二次运动,向右运动 2个单位长度,在此位置第三次运动,向左运动 3个单位长度…按照如此规律不断地左右运动,当运动到 2019次时,求点P所对应的数.
(3)在(2)的条件下,点 P在某次运动时恰好到达某一个位置,使点 P到点B的距离是点 P 到点 A 的距离的3倍?请直接写出此时点 P所对应的数,并分别写出是第几次运动.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校八年级有800名学生,在体育中考前进行一次排球模拟测试,从中随机抽取部分学生,根据其测试成绩制作了下面两个统计图,请根据相关信息,解答下列问题:

(1)本次抽取到的学生人数为________,图2中![]() 的值为_________.
的值为_________.
(2)本次调查获取的样本数据的平均数是__________,众数是________,中位数是_________.
(3)根据样本数据,估计我校八年级模拟体测中得12分的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
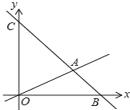
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的![]() ?若存在求出此时点M的坐标;若不存在,说明理由.
?若存在求出此时点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从![]() 地出发,匀速驶向
地出发,匀速驶向![]() 地.甲车以
地.甲车以![]() 的速度行驶
的速度行驶![]() 后,乙车才沿相同路线行驶.乙车先到达
后,乙车才沿相同路线行驶.乙车先到达![]() 地并停留
地并停留![]() 后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离
后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离![]() 与乙车行驶时间
与乙车行驶时间![]() 之间的函数关系如图所示.下列说法:①乙车的速度是
之间的函数关系如图所示.下列说法:①乙车的速度是![]() ;②
;②![]() ;③点
;③点![]() 的坐标是
的坐标是![]() ;④
;④![]() .其中说法正确的是_________.
.其中说法正确的是_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】班级组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动,基地离学校有90公里,队伍8:00从学校出发.苏老师因有事情,8:30从学校自驾小车以大巴1.5倍的速度追赶,追上大巴后继续前行,结果比队伍提前15分钟到达基地.问:
(1)大巴与小车的平均速度各是多少?
(2)苏老师追上大巴的地点到基地的路程有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,…则第n个图形有__个小圆.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 交x轴于点A,交直线
交x轴于点A,交直线![]() 于点B(2,m).矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴的上方,DC=2,DE=4.当点C的坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.(注:矩形就是长方形)
于点B(2,m).矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴的上方,DC=2,DE=4.当点C的坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.(注:矩形就是长方形)
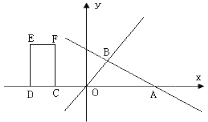
(1)求b、m的值;
(2)当矩形CDEF运动t秒时,请直接写出C、D两点的坐标(用含t的代数式表示)
(3)当点B在矩形CDEF的一边上时,求t的值;
(4)设CF、DE分别交折线OBA于M、N两点,当四边形MCDN为直角梯形时,求t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com