
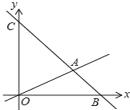
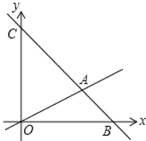
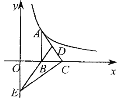
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的![]() ?若存在求出此时点M的坐标;若不存在,说明理由.
?若存在求出此时点M的坐标;若不存在,说明理由.
【答案】(1)y=﹣x+6;(2)S△OAC=12;(3)存在,M的坐标是:M1(1,![]() )或M2(1,5)或M3(﹣1,7)
)或M2(1,5)或M3(﹣1,7)
【解析】
(1)利用待定系数法即可求得函数的解析式;
(2)求得C的坐标,即OC的长,利用三角形的面积公式即可求解;
(3)当△OMC的面积是△OAC的面积的![]() 时,根据面积公式即可求得M的横坐标,然后代入解析式即可求得M的坐标.
时,根据面积公式即可求得M的横坐标,然后代入解析式即可求得M的坐标.
解:(1)设直线AB的解析式是![]() ,
,
根据题意得:![]() ,
,
解得:![]() ,
,
则直线的解析式是:![]() ;
;
(2)在y=﹣x+6中,令x=0,解得:y=6,
![]() ;
;
(3)设OA的解析式是y=mx,则4m=2,
解得:![]() ,
,
则直线的解析式是:![]() ,
,
∵当△OMC的面积是△OAC的面积的![]() 时,
时,
∴当M的横坐标是![]() ,
,
在![]() 中,当x=1时,y=
中,当x=1时,y=![]() ,则M的坐标是
,则M的坐标是![]() ;
;
在![]() 中,x=1则y=5,则M的坐标是(1,5).
中,x=1则y=5,则M的坐标是(1,5).
则M的坐标是:M1(1,![]() )或M2(1,5).
)或M2(1,5).
当M的横坐标是:﹣1,
在![]() 中,当x=﹣1时,y=7,则M的坐标是(﹣1,7);
中,当x=﹣1时,y=7,则M的坐标是(﹣1,7);
综上所述:M的坐标是:M1(1,![]() )或M2(1,5)或M3(﹣1,7).
)或M2(1,5)或M3(﹣1,7).


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=3,CD=4,点P是AC上一个动点(点P与点A,C不重合),过点P分别作PE⊥BC于点E,PF∥BC交AB于点F,连接EF,则EF的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE是⊙O的直径,点A在EB的延长线上,弦PD⊥BE,垂足为C,连接OD,∠AOD=∠APC.

(1)求证:AP是⊙O的切线;
(2)若⊙O的半径是4,AP=4![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初中生对待学习的态度一直是教育工作者关注的问题之一.为此市教育局对部分学校的九年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1) 此次抽样调查中,共调查了 名学生;并将图①补充完整;
(2) 求出图中②C级所占的圆心角的度数;
(3) 根据抽样调查结果,请你估计我市近50000名九年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?
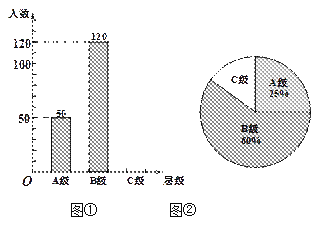
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校运动会需购买A,B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.
(1)求A、B两种奖品的单价各是多少元?
(2)学校计划购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式.求出自变量m的取值范围,并确定最少费用W的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,BC=12,E为边AC的中点,
(1)如图1,过点E作EH⊥BC,垂足为点H,求线段CH的长;
(2)作线段BE的垂直平分线分别交边BC、BE、AB于点D、O、F.
①如图2,当∠BAC=90°时,求BD的长;
②如图3,设tan∠ACB=x,BD=y,求y与x之间的函数表达式和tan∠ACB的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
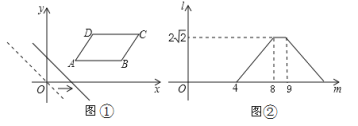
【题目】如图①,在平面直角坐标系中,将□ABCD放置在第一象限,且AB∥x轴,直线y=-x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图②所示,那么AD的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 若|a|=﹣a,则a<0
B. 式子3xy2﹣43x3y+12是七次三项式
C. 若a=b,m是有理数,则![]()
D. 若abcd<0,a+b=0,cd>0,那么这四个数中负因数的个数至少有1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC边上的中线BD的反向延长线交y轴负半轴于点E,双曲线![]() 的图象经过点A,若S△BEC=3,则k等于( )
的图象经过点A,若S△BEC=3,则k等于( )
A.12B.6C.3D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com