
【题目】
(1)解方程: ![]()
(2)解不等式:2(x﹣6)+4≤3x﹣5,并将它的解集在数轴上表示出来. ![]()
【答案】
(1)解:去分母得:x=3(x﹣3),
解得:x= ![]() ,
,
检验:x= ![]() 时,x(x﹣3)≠0,则x=
时,x(x﹣3)≠0,则x= ![]() 是原方程的根
是原方程的根
(2)解:2(x﹣6)+4≤3x﹣5
2x﹣12+4≤3x﹣5,
解得:x≥﹣3,
如图所示:
![]() .
.
【解析】(1)首先找出最简公分母,再去分母进而解方程得出答案;(2)首先去括号,进而解不等式得出答案.
【考点精析】掌握去分母法和不等式的解集在数轴上的表示是解答本题的根本,需要知道先约后乘公分母,整式方程转化出.特殊情况可换元,去掉分母是出路.求得解后要验根,原留增舍别含糊;不等式的解集可以在数轴上表示,分三步进行:①画数轴②定界点③定方向.规律:用数轴表示不等式的解集,应记住下面的规律:大于向右画,小于向左画,等于用实心圆点,不等于用空心圆圈.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,P是反比例函数y= ![]() (x>0)图象上的任意一点,以P为圆心,PO为半径的圆与x、y轴分别交于点A、B.
(x>0)图象上的任意一点,以P为圆心,PO为半径的圆与x、y轴分别交于点A、B.
(1)判断P是否在线段AB上,并说明理由;
(2)求△AOB的面积;
(3)Q是反比例函数y= ![]() (x>0)图象上异于点P的另一点,请以Q为圆心,QO半径画圆与x、y轴分别交于点M、N,连接AN、MB.求证:AN∥MB.
(x>0)图象上异于点P的另一点,请以Q为圆心,QO半径画圆与x、y轴分别交于点M、N,连接AN、MB.求证:AN∥MB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l经过点A(1,0),与双曲线y= ![]() (x>0)交于点B(2,1).过点P(p,p﹣1)(p>1)作x轴的平行线分别交双曲线y=
(x>0)交于点B(2,1).过点P(p,p﹣1)(p>1)作x轴的平行线分别交双曲线y= ![]() (x>0)和y=﹣
(x>0)和y=﹣ ![]() (x<0)于点M、N.
(x<0)于点M、N. 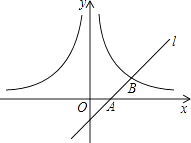
(1)求m的值和直线l的解析式;
(2)若点P在直线y=2上,求证:△PMB∽△PNA;
(3)是否存在实数p,使得S△AMN=4S△AMP?若存在,请求出所有满足条件的p的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y= ![]() x﹣3与反比例函数
x﹣3与反比例函数 ![]() 的图象相交于点A(4,n),与
的图象相交于点A(4,n),与 ![]() 轴相交于点B.
轴相交于点B.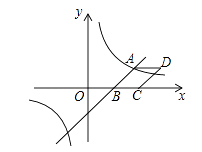
(1)填空:n的值为 , k的值为;
(2)以AB为边作菱形ABCD,使点C在 ![]() 轴正半轴上,点D在第一象限,求点D的坐标;
轴正半轴上,点D在第一象限,求点D的坐标;
(3)考察反比函数 ![]() 的图象,当
的图象,当 ![]() 时,请直接写出自变量
时,请直接写出自变量 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果三角形三边的长a、b、c满足 ![]() =b,那么我们就把这样的三角形叫做“匀称三角形”,如:三边长分别为1,1,1或3,5,7,…的三角形都是“匀称三角形”.
=b,那么我们就把这样的三角形叫做“匀称三角形”,如:三边长分别为1,1,1或3,5,7,…的三角形都是“匀称三角形”. 
(1)如图1,已知两条线段的长分别为a、c(a<c).用直尺和圆规作一个最短边、最长边的长分别为a、c的“匀称三角形”(不写作法,保留作图痕迹);
(2)如图2,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线交AB延长线于点E,交AC于点F,若 ![]() ,判断△AEF是否为“匀称三角形”?请说明理由.
,判断△AEF是否为“匀称三角形”?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的边长2,∠A=60°,点E、F分别在边AB、AD上,若将△AEF沿直线EF折叠,使得点A恰好落在CD边的中点G处,则EF= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,点P在射线BC上(异于点B、C),直线AP与对角线BD及射线DC分别交于点F、Q 
(1)若BP= ![]() ,求∠BAP的度数;
,求∠BAP的度数;
(2)若点P在线段BC上,过点F作FG⊥CD,垂足为G,当△FGC≌△QCP时,求PC的长;
(3)以PQ为直径作⊙M. ①判断FC和⊙M的位置关系,并说明理由;
②当直线BD与⊙M相切时,直接写出PC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com