
【题目】如图,已知一次函数y= ![]() x﹣3与反比例函数
x﹣3与反比例函数 ![]() 的图象相交于点A(4,n),与
的图象相交于点A(4,n),与 ![]() 轴相交于点B.
轴相交于点B.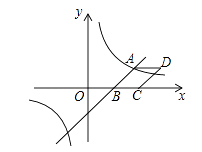
(1)填空:n的值为 , k的值为;
(2)以AB为边作菱形ABCD,使点C在 ![]() 轴正半轴上,点D在第一象限,求点D的坐标;
轴正半轴上,点D在第一象限,求点D的坐标;
(3)考察反比函数 ![]() 的图象,当
的图象,当 ![]() 时,请直接写出自变量
时,请直接写出自变量 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:把点A(4,n)代入一次函数y=![]() x﹣3,可得n=
x﹣3,可得n=![]() ×4﹣3=3;;把点A(4,3)代入反比例函数y=
×4﹣3=3;;把点A(4,3)代入反比例函数y=![]() , 可得3=
, 可得3=![]() , 解得k=12;
, 解得k=12;
(2)
解:∵一次函数y=![]() x﹣3与x轴相交于点B,
x﹣3与x轴相交于点B,
∴![]() x﹣3=0,
x﹣3=0,
解得x=2,
∴点B的坐标为(2,0);
如图,过点A作AE⊥x轴,垂足为E,过点D作DF⊥x轴,垂足为F,
∵A(4,3),B(2,0),
∴OE=4,AE=3,OB=2,
∴BE=OE﹣OB=4﹣2=2,
在Rt△ABE中,AB=![]() =
=![]() =
=![]() ,
,
∵四边形ABCD是菱形,
∴AB=CD=BC=![]() ,
,
∵AB∥CD,
∴∠ABE=∠DCF,
∵AE⊥x轴,DF⊥x轴,
∴∠AEB=∠DFC=90°,
在△ABE与△DCF中,
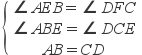
∴△ABE≌△DCF(ASA),
∴CF=BE=2,DF=AE=3;
∴OF=OB+BC+CF=2+![]() +2=4+
+2=4+![]() ,
,
∴点D的坐标为(4+![]() ,3)
,3)

(3)
解:当y=﹣2时,﹣2=![]() ,解得x=﹣6.
,解得x=﹣6.
故当y≥﹣2时,自变量x的取值范围是x≤﹣6或x>0.
【解析】(1)把点A(4,n)代入一次函数y= ![]() x﹣3,可得n的值;把点A(4,3)代入反比例函数y=
x﹣3,可得n的值;把点A(4,3)代入反比例函数y=![]() ,可得k的值;
,可得k的值;
(2)求出一次函数y=![]() x﹣3与x轴的交点B的坐标(2,0);如图,过点A作AE⊥x轴,垂足为E,过点D作DF⊥x轴,垂足为F再根据勾股定理,菱形的性质,得出△ABE≌△DCF(ASA),由全等三角形的性质求出答案。
x﹣3与x轴的交点B的坐标(2,0);如图,过点A作AE⊥x轴,垂足为E,过点D作DF⊥x轴,垂足为F再根据勾股定理,菱形的性质,得出△ABE≌△DCF(ASA),由全等三角形的性质求出答案。
(3)当y=﹣2时,﹣2=![]() ,解得x=﹣6.故当y≥﹣2时,自变量x的取值范围是x≤﹣6或x>0.
,解得x=﹣6.故当y≥﹣2时,自变量x的取值范围是x≤﹣6或x>0.
【考点精析】掌握反比例函数的性质和菱形的性质是解答本题的根本,需要知道性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,计算出甲的平均成绩是环,乙的平均成绩是环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由. (计算方差的公式:s2= ![]() [
[ ![]() ])
])
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三个半圆依次相外切,它们的圆心都在x轴上,并与直线y= ![]() x相切.设三个半圆的半径依次为r1、r2、r3 , 则当r1=1时,r3= .
x相切.设三个半圆的半径依次为r1、r2、r3 , 则当r1=1时,r3= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从3名男生和2名女生中随机抽取2014年南京青奥会志愿者.求下列事件的概率:
(1)抽取1名,恰好是女生;
(2)抽取2名,恰好是1名男生和1名女生.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若点P(a,b)在函数y= ![]() 的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y=的一个“派生函数”.例如:点(2,
的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y=的一个“派生函数”.例如:点(2, ![]() )在函数y=
)在函数y= ![]() 的图象上,则函数y=2x2+x称为函数y=
的图象上,则函数y=2x2+x称为函数y= ![]() 的一个“派生函数”.现给出以下两个命题:(1)存在函数y=
的一个“派生函数”.现给出以下两个命题:(1)存在函数y= ![]() 的一个“派生函数”,其图象的对称轴在y轴的右侧;(2)函数y=
的一个“派生函数”,其图象的对称轴在y轴的右侧;(2)函数y= ![]() 的所有“派生函数”的图象都经过同一点.下列判断正确的是( )
的所有“派生函数”的图象都经过同一点.下列判断正确的是( )
A.命题(1)与命题(2)都是真命题
B.命题(1)与命题(2)都是假命题
C.命题(1)是假命题,命题(2)是真命题
D.命题(1)是真命题,命题(2)是假命题
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y1=(x﹣2)(x﹣4)的图象与x轴交于A、B两点(点A在点B的左侧),其对称轴l与x轴交于点C,它的顶点为点D.
(1)写出点D的坐标 .
(2)点P在对称轴l上,位于点C上方,且CP=2CD,以P为顶点的二次函数y2=ax2+bx+c(a≠0)的图象过点A.
试说明二次函数y2=ax2+bx+c(a≠0)的图象过点B;
(3)点R在二次函数y1=(x﹣2)(x﹣4)的图象上,到x轴的距离为d,当点R的坐标为时,二次函数y2=ax2+bx+c(a≠0)的图象上有且只有三个点到x轴的距离等于2d;
(4)如图2,已知0<m<2,过点M(0,m)作x轴的平行线,分别交二次函数y1=(x﹣2)(x﹣4)、y2=ax2+bx+c(a≠0)的图象于点E、F、G、H(点E、G在对称轴l左侧),过点H作x轴的垂线,垂足为点N,交二次函数y1=(x﹣2)(x﹣4)的图象于点Q,若△GHN∽△EHQ,求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O 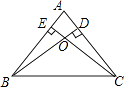
(1)求证:OB=OC;
(2)若∠ABC=50°,求∠BOC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com