
【题目】从3名男生和2名女生中随机抽取2014年南京青奥会志愿者.求下列事件的概率:
(1)抽取1名,恰好是女生;
(2)抽取2名,恰好是1名男生和1名女生.
【答案】
(1)解:5名学生中有2名女生,所以抽取1名,恰好是女生的概率为 ![]()
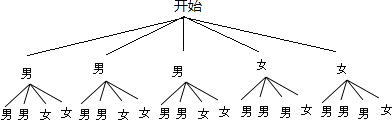
(2)解:由树形图可得出:共有20种情况,恰好是1名男生和1名女生的情况数有12种,所以概率为 ![]() .
. 
【解析】(1)女生人数除以学生总数即为所求概率;(2)列举出所有情况,看恰好是1名男生和1名女生的情况数占总情况数的多少即可.
【考点精析】掌握列表法与树状图法和概率公式是解答本题的根本,需要知道当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率;一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n.


 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】根据第5次、第6次人口普查的结果,2000年,2010年我国每10万人受教育程度的情况如下: 
根据图中的信息,完成下列填空:
(1)2010年我国具有高中文化程度的人口比重为;
(2)2010年我国具有文化程度的人口最多;
(3)同2000年相比,2010年我国具有文化程度的人口增幅最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l经过点A(1,0),与双曲线y= ![]() (x>0)交于点B(2,1).过点P(p,p﹣1)(p>1)作x轴的平行线分别交双曲线y=
(x>0)交于点B(2,1).过点P(p,p﹣1)(p>1)作x轴的平行线分别交双曲线y= ![]() (x>0)和y=﹣
(x>0)和y=﹣ ![]() (x<0)于点M、N.
(x<0)于点M、N. 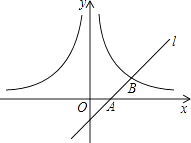
(1)求m的值和直线l的解析式;
(2)若点P在直线y=2上,求证:△PMB∽△PNA;
(3)是否存在实数p,使得S△AMN=4S△AMP?若存在,请求出所有满足条件的p的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F分别是正方形ABCD的边BC、CD上的点,BE=CF,连接AE、BF.将△ABE绕正方形的中心按逆时针方向旋转到△BCF,旋转角为α( 0°<α<180°),则∠α= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y= ![]() x﹣3与反比例函数
x﹣3与反比例函数 ![]() 的图象相交于点A(4,n),与
的图象相交于点A(4,n),与 ![]() 轴相交于点B.
轴相交于点B.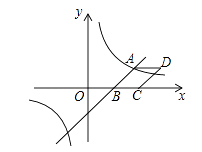
(1)填空:n的值为 , k的值为;
(2)以AB为边作菱形ABCD,使点C在 ![]() 轴正半轴上,点D在第一象限,求点D的坐标;
轴正半轴上,点D在第一象限,求点D的坐标;
(3)考察反比函数 ![]() 的图象,当
的图象,当 ![]() 时,请直接写出自变量
时,请直接写出自变量 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的边长2,∠A=60°,点E、F分别在边AB、AD上,若将△AEF沿直线EF折叠,使得点A恰好落在CD边的中点G处,则EF= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AM为⊙O的切线,A为切点,过⊙O上一点B作BD⊥AM于点D,BD交⊙O于点C,OC平分∠AOB. 
(1)求∠AOB的度数;
(2)当⊙O的半径为2cm,求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com