练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

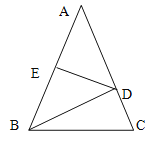
    【题目】如图：△ABC中，AB=AC=5，AB的垂直平分线DE交AB、AC于E、D，

    ① 若△BCD的周长为8，求BC的长；

    ② 若BC=4，求△BCD的周长．

    【答案】(1)、BC=3；(2)、周长为9.

    【解析】

    试题分析：(1)、根据中垂线的性质得出BD=AD，根据△BCD的周长以及AC的长度得到BC的长度；(2)、同第一题同样的方法求出△BCD的周长.

    试题解析： ① ∵DE是AB的垂直平分线 ∴ BD=AD

    ∴△BCD的周长为:BD+DC+BC=AD+CD+BC=AC+BC=8 ∵AB=AC=5 ∴BC=8-5=3

    ②∵DE是AB的垂直平分线 ∴BD=AD ∴ △BCD的周长为：BC+BD+CD=AD+CD+BC=AC+BC=4+5=9

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】罗马数字共有 7 个：I（表示 1），V（表示 5），X（表示 10），L（表示 50），C（表示 100），D（表示 500），M（表示 1000），这些数字不论位置怎样变化，所表示的数目都是不变的，其计数方法是用“累积符号”和“前减后加”的原则来计数的：如IX＝10－1＝9，VI＝5＋1＝6，CD＝500－100＝400，则XL＝ ，XI＝ ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果收入50元记作+50元，那么支出20元可记作（　　）．

    A．+20元 B．-20元 C．+70元 D．-70元

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】完成下面的证明.

    （1）如图，AB∥CD，CB∥DE.求证：∠B+∠D=180°.

    证明：∵AB∥CD，

    ∴∠B=（ ① ）（ ② ）；

    ∵CB∥DE，

    ∴∠C+∠D=180°（ ③ ）.

    ∴∠B+∠D=180°.

    （2）如图，∠ABC=∠A′B′C′，BD，B′D′分别是∠ABC，∠A′B′C′的平分线.求证:∠1=∠2.

    证明：∵BD， B′D′分别是∠ABC，∠A′B′C′的平分线，

    ∴∠1=∠ABC，∠2=（ ④ ）（ ⑤ ）.

    又∠ABC=∠A′B′C′，

    ∴∠ABC=∠A′B′C′.

    ∴∠1=∠2（ ⑥ ）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】与点 P (a＋2，－a－1)在同一个象限内的点是( )

    A. （2，－1）B. （－1，2）C. （－2，－1）D. （2，1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个三角形三边满足（a+b）2﹣c2=2ab，则这个三角形是 三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数据0，-1，-2，2，1，这组数据的中位数是( )

    A.-2B.2C.0.5D.0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙、丙、丁四人进行射箭测试，每人10次，测试成绩的平均数都是8.9环，方差分别是s甲2＝0.45，s乙2＝0.50，s丙2＝0.55，s丁2＝0.65，则测试成绩最稳定的是（ ）

    A.甲B.乙C.丙D.丁

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点(-1，y1)，(4，y2)，(5，y3)都在抛物线y＝(x-3)2+k上，则y1，y2，y3的大小关系为（ ）

    A. y1＜y2＜y3 B. y1＜y3＜y2 C. y1＞y2＞y3 D. y1＞y3＞y2

    查看答案和解析>>

    同步练习册答案