
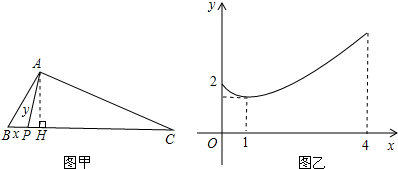
分析 (1)当x取0时,y的值即是AB的长度,图乙函数图象的最低点的y值是AH的值;
(2)在直角△ACH中,由勾股定理来求AC的长度;
解答 解:(1)当x=0时,y的值即是AB的长度,故AB=2;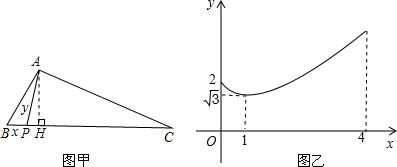
图乙函数图象的最低点的y值是AH的值,故AH=$\sqrt{3}$,
故答案是:2;$\sqrt{3}$;
(2)如图乙所示:依题意得BC=4,BP=1,
由(1)得AB=2,AP=$\sqrt{3}$,
∴PC=BC-BP=4-1=3,
在Rt△APC中,AC=$\sqrt{A{P}^{2}+P{C}^{2}}$=$\sqrt{3+9}$=2$\sqrt{3}$.
点评 此题考查了动点问题的函数图象,有一定难度,解答本题的关键是结合图象及函数图象得出AB、AH的长度.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:选择题
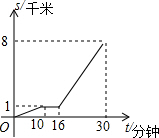 小亮从家步行到公交站台,等公交去学校,图中的折线表示小亮的行程s(千米)与所花时间t(分钟)之间的函数关系.下列说法错误的是( )
小亮从家步行到公交站台,等公交去学校,图中的折线表示小亮的行程s(千米)与所花时间t(分钟)之间的函数关系.下列说法错误的是( )| A. | 小亮行程8千米,共用了30分钟 | B. | 小亮等公交车时间为6分钟 | ||
| C. | 小亮步行的速度是100米/分钟 | D. | 公交车的速度是350米/分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
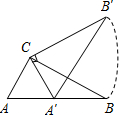 三角板ABC中,∠ACB=90°,∠B=30°,AC=2$\sqrt{3}$,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( )
三角板ABC中,∠ACB=90°,∠B=30°,AC=2$\sqrt{3}$,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( )| A. | $\frac{3}{2}$π | B. | $\frac{4}{3}$$\sqrt{3}$π | C. | 2π | D. | 3π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知∠AOB=60°,点P在边OA上,OP=20,点M,N在边OB上,PM=PN.若MN=6,则OM=( )
如图,已知∠AOB=60°,点P在边OA上,OP=20,点M,N在边OB上,PM=PN.若MN=6,则OM=( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com