
【题目】如图,直线l:y=﹣2x+m与x轴交于点A(﹣2,0),抛物线C1:y=x2+4x+3与x轴的一个交点为B(点B在点A的左侧),过点B作BD垂直x轴交直线l于点 D.
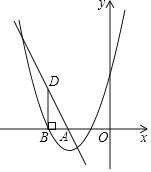
(1)求m的值和点B的坐标;
(2)将△ABD绕点A顺时针旋转90°,点B,D的对应点分别为点E,F.
①点F的坐标为 ;
②将抛物线C1向右平移使它经过点F,此时得到的抛物线记为C2,直接写出抛物线C2的表达式.
【答案】(1)m=﹣4,点B的坐标为(﹣3,0);(2)①(0,1);②y=x2﹣2![]() x+1或y=x2+2
x+1或y=x2+2![]() x+1.
x+1.
【解析】
(1)由点A的坐标,利用待定系数法即可求出m的值,再利用二次函数图象上点的坐标特征结合点B在点A的左侧,即可求出点B的坐标;
(2)利用一次函数图象上点的坐标特征可得出点D的坐标,进而可得出BD,AB的值.
①依照题意画出图形,由EF=BD=2,OF=AE=AB=1可得出点F在y轴正半轴上,进而可求出点F的坐标;
②利用配方程法将抛物线C1的表达式变形为顶点式,根据平移的性质可设抛物线C2的表达式为y=(x+m)2﹣1,由点F的坐标,利用待定系数法即可求出抛物线C2的表达式,此题得解.
解:(1)将A(﹣2,0)代入y=﹣2x+m,得:0=﹣2×(﹣2)+m,
解得:m=﹣4.
当y=0时,有x2+4x+3=0,
解得:x1=﹣3,x2=﹣1,
又∵点B在点A的左侧,
∴点B的坐标为(﹣3,0).
(2)当x=﹣3时,y=﹣2x﹣4=2,
∴点D的坐标为(﹣3,2),
∴BD=2,AB=1.
①依照题意画出图形,则EF=BD=2,OF=AE=AB=1,
又∵点A的坐标为(﹣2,0),
∴点F在y轴正半轴上,
∴点F的坐标为(0,1).
②∵y=x2+4x+3=(x+2)2﹣1,
∴设平移后得到的抛物线C2的表达式为y=(x+m)2﹣1.
将F(0,1)代入y=(x+m)2﹣1,得:1=(0+m)2﹣1,
解得:m1=![]() ,m2=﹣
,m2=﹣![]() ,
,
∴抛物线C2的表达式为y=(x﹣![]() )2﹣1或y=(x+
)2﹣1或y=(x+![]() )2﹣1,即y=x2﹣2
)2﹣1,即y=x2﹣2![]() x+1或y=x2+2
x+1或y=x2+2![]() x+1.
x+1.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一个抛物线形状与二次函数y=x2的图象形状和顶点相同,但开口方向不同.
(1)求抛物线解析式.
(2)如果该抛物线与一次函数y=kx﹣2相交于A、B两点,已知A点的纵坐标为﹣1,求△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:![]() .
.
(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?
(成本=进价×销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线y=ax+b与抛物线![]() 的一个交点为(0,2),同时这条直线与x轴相交于点A,且相交所成的角为45°.
的一个交点为(0,2),同时这条直线与x轴相交于点A,且相交所成的角为45°.
(1)点A的坐标为__________;
(2)若抛物线![]() 与x轴交于点M、N(点M在点N左边),将此抛物线作关于y轴对称,M的对应点为E,两抛物线相交于点F,连接NF,EF得△NEF,P是轴对称后的抛物线上的点,使得△NEP的面积与△NEF的面积相等,则P点坐标为_________.
与x轴交于点M、N(点M在点N左边),将此抛物线作关于y轴对称,M的对应点为E,两抛物线相交于点F,连接NF,EF得△NEF,P是轴对称后的抛物线上的点,使得△NEP的面积与△NEF的面积相等,则P点坐标为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
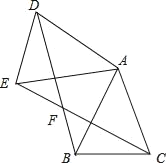
(1)求证:△AEC≌△ADB;(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三江超市为了吸引顾客,设计了一种促销活动,在一个不透明的箱子里放有4个相同小球,在球上分别标有“0元”、“10元”、“20元”、“30元”的字样,规定:顾客每消费满298元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).超市根据两小球所标金额的和,返还相应价格的购物券.某顾客正好消费298元.
(1)该顾客至少可得到 元购物券,至多可得到 元购物券.
(2)请用画树状图或列表的方法,求出该顾客所获得购物券不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x与双曲线y=![]() 在第一象限的交点为A,过点A作AB⊥x轴,垂足为B,将△ABO绕点O逆时针旋转90°,得到△A′B′O(点A对应点A′),则点A′的坐标是( )
在第一象限的交点为A,过点A作AB⊥x轴,垂足为B,将△ABO绕点O逆时针旋转90°,得到△A′B′O(点A对应点A′),则点A′的坐标是( )
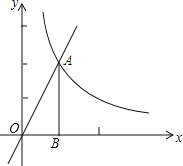
A.(2,0) B.(2,﹣1) C.(﹣2,1) D.(﹣1,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=-x2+bx+c经过点(0,6),其对称轴为直线x=![]() .在x轴上方作平行于x轴的直线l与抛物线交于A、B两点(点A在对称轴的右侧),过点A、B作x轴的垂线,垂足分别为D、C.设A点的横坐标为m.
.在x轴上方作平行于x轴的直线l与抛物线交于A、B两点(点A在对称轴的右侧),过点A、B作x轴的垂线,垂足分别为D、C.设A点的横坐标为m.

(1)求此抛物线所对应的函数关系式.
(2)当m为何值时,矩形ABCD为正方形.
(3)当m为何值时,矩形ABCD的周长最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,2)与(0,3)之间(不包括这两点),对称轴为直线x=2.下列结论:
①abc<0;②9a+3b+c>0;③若点M(![]() ,y1),点N(
,y1),点N(![]() ,y2)是函数图象上的两点,则y1>y2;④﹣
,y2)是函数图象上的两点,则y1>y2;④﹣![]() <a<﹣
<a<﹣![]() ;⑤c-3a>0.
;⑤c-3a>0.
其中正确结论有( )
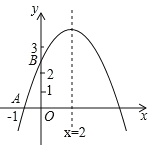
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com