
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,2)与(0,3)之间(不包括这两点),对称轴为直线x=2.下列结论:
①abc<0;②9a+3b+c>0;③若点M(![]() ,y1),点N(
,y1),点N(![]() ,y2)是函数图象上的两点,则y1>y2;④﹣
,y2)是函数图象上的两点,则y1>y2;④﹣![]() <a<﹣
<a<﹣![]() ;⑤c-3a>0.
;⑤c-3a>0.
其中正确结论有( )
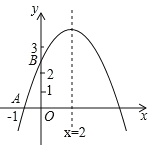
A.1个B.2个C.3个D.4个
【答案】D
【解析】
①根据二次函数图像与系数的关系可知:开口向下,a<0;对称轴在y轴右侧,根据“左同右异”可知a、b异号,则b>0;图像与y轴交于正半轴,则c>0,据此可判断;
②根据抛物线对称性,可得图像与x轴的另一交点为(5,0),由图像可知当x=3时,y>0,可判断;
③找出N(![]() ,y2)关于对称轴的对称点,再用二次函数的增减性判断大小;
,y2)关于对称轴的对称点,再用二次函数的增减性判断大小;
④根据对称轴x=2,可得![]() ,将(-1,0)代入函数解析式可得
,将(-1,0)代入函数解析式可得![]() ,最后B在(0,2)与(0,3)之间可判断a的取值范围.
,最后B在(0,2)与(0,3)之间可判断a的取值范围.
⑤由![]() ,可得
,可得![]() .
.
①抛物线开口向上,∴![]()
对称轴![]() ,∴
,∴![]() (左同右异)
(左同右异)
抛物线与y轴交于正半轴,∴![]()
∴abc<0,故①正确;
②∵图象与x轴交于点A(﹣1,0),对称轴为直线x=2,
∴图像与x轴的另一交点为(5,0),当x=3时,y>0,
∴9a+3b+c>0,故②正确;
③N(![]() ,y2)关于对称轴x=2的对称点为(
,y2)关于对称轴x=2的对称点为(![]() ,y2),
,y2),
![]() ,根据抛物线图像可知在对称轴左侧,y随x的增大而增大,
,根据抛物线图像可知在对称轴左侧,y随x的增大而增大,
∴y1<y2,故③错误;
④对称轴![]() ,∴
,∴![]() ,
,
将(-1,0)代入二次函数可得![]() ,∴
,∴![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ,解得﹣
,解得﹣![]() <a<﹣
<a<﹣![]() ,故④正确;
,故④正确;
⑤由④中![]() 可得
可得![]() ,故⑤正确.
,故⑤正确.
所以选D.


 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,直线l:y=﹣2x+m与x轴交于点A(﹣2,0),抛物线C1:y=x2+4x+3与x轴的一个交点为B(点B在点A的左侧),过点B作BD垂直x轴交直线l于点 D.
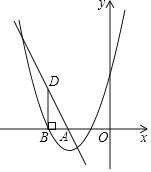
(1)求m的值和点B的坐标;
(2)将△ABD绕点A顺时针旋转90°,点B,D的对应点分别为点E,F.
①点F的坐标为 ;
②将抛物线C1向右平移使它经过点F,此时得到的抛物线记为C2,直接写出抛物线C2的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着经济的快速发展,环境问题越来越受到人们的关注,某校学生会为了解节能减排、垃圾分类知识
的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,
并将检查结果绘制成下面两个统计图.
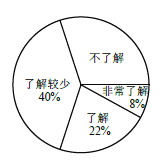

(1)本次调查的学生共有__________人,估计该校1200 名学生中“不了解”的人数是__________人.
(2)“非常了解”的4 人有![]() 两名男生,
两名男生,![]() 两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
(1)求抛物线的解析式;
(2)求△MCB的面积.
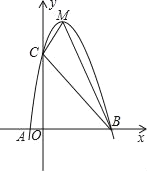
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AD//BC,AD=2,AB=5,BC=10,点E是边BC上的一个动点(不与B,C重合),作∠AEF=∠AEB,使边EF交边CD于点F,(不与C,D重合),线段BE=______________时,△ABE与△CEF相似。
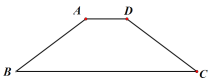
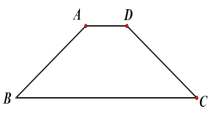
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴正半轴交于点A(3,0).以OA为边在
轴正半轴交于点A(3,0).以OA为边在![]() 轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,则
轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,则![]() = ,点E的坐标是 .
= ,点E的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为每件![]() 元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于
元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于![]() ,经试销发现,销售量
,经试销发现,销售量![]() (件)与销售单价
(件)与销售单价![]() (元)符合一次函数,所调查的部分数据如表:
(元)符合一次函数,所调查的部分数据如表:
销售单价 | 60 | 65 | 70 |
|
销售量 | 60 | 55 | 50 |
|
(1)求出![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)若该商场获得利润为![]() 元,试写出利润
元,试写出利润![]() 与销售单价
与销售单价![]() 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少?
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少?
(3)销售单价定为多少元时,该商场获得的利润恰为![]() 元?
元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com