练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知反比例函数y=(m-1) 的图象在第二、四象限，求m的值，并指出在每个象限内y随x的变化情况.


    ∵y=(m-1)xm2-3是反比例函数，

    ∴m2-3＝-1，且m-1≠0.解得m=±.

    又∵图象在第二、四象限，∴m-1＜0，即m＜1.

    ∴m=-.

    在每个象限内，y随着x的增大而增大.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    点A(1，-2)关于x轴对称的点的坐标是(     )

      A.(1，-2)             B.(-1，2)              C.(-1，-2)              D.(1，2)

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若点A(-2，m)在正比例函数y=-x的图象上，则m的值是(     )

      A.                B.-                   C.1                   D.-1

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一次函数y=kx+b，当3≤x≤4时，3≤y≤6，则的值是           .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    反比例函数y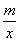＝的图象如图所示，以下结论：①常数m＜-1；②在每个象限内，y随x的增大而增大；③若A(-1，h)，B(2，k)在图象上，则h＜k；④若P(x，y)在图象上，则P′(-x，-y)也在图象上.其中正确的是(     )

      A.①②             B.②③            C.③④            D.①④

    查看答案和解析>>

    科目：初中数学 来源： 题型：


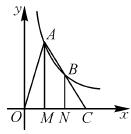
    如图，点A、B在反比例函数y=(k>0,x>0)的图象上，过点A、B作x轴的垂线，垂足分别为M、N，延长线段AB交x轴于点C，若OM=MN=NC,△AOC的面积为6，则k的值为          .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


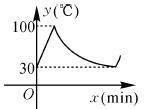
    教室里的饮水机接通电源就进入自动程序：开机加热时每分钟上升10 ℃，加热到100 ℃后停止加热，水温开始下降，此时水温(℃)与开机后用时(min)成反比例关系，直至水温降至30 ℃，饮水机关机.饮水机关机后即刻自动开机，重复上述自动程序.若在水温为30 ℃时，接通电源后，水温y(℃)和时间x(min)的关系如右图，为了在上午第一节下课时(8:45)能喝到不超过50 ℃的水，则接通电源的时间可以是当天上午的(     )

      A.7:20           B.7:30             C.7:45                 D.7:50

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知反比例函数y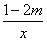＝(m为常数)的图象在一、三象限.

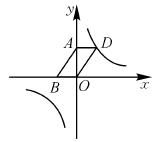
    (1)求m的取值范围；

    (2)如图，若该反比例函数的图象经过□ABOD的顶点D，点A，B的坐标分别为(0，3)，(-2，0).

    ①求出函数解析式；

    ②设点P是该反比例函数图象上的一点，若OD＝OP，则P点的坐标为                .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，小河上有一拱桥，拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE,ED,DB组成，已知河底ED是水平的，ED=16米，AE=8米，抛物线的顶点C到ED距离是11米，以ED所在的直线为x轴，抛物线的对称轴为y轴建立平面直角坐标系.

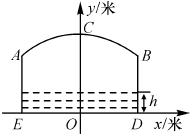
    (1)求抛物线的解析式；

    (2)已知从某时刻开始的40小时内，水面与河底ED的距离h(单位：米)随时间ｔ(单位：时)的变化满足函数关系

    h=-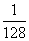(t-19)2+8(0≤t≤40)且当水面到顶点C的距离不大于5米时，需禁止船只通行，请通过计算说明：在这一时段内，需多少小时禁止船只通行？

    查看答案和解析>>

    同步练习册答案