练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，小河上有一拱桥，拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE,ED,DB组成，已知河底ED是水平的，ED=16米，AE=8米，抛物线的顶点C到ED距离是11米，以ED所在的直线为x轴，抛物线的对称轴为y轴建立平面直角坐标系.

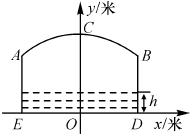
    (1)求抛物线的解析式；

    (2)已知从某时刻开始的40小时内，水面与河底ED的距离h(单位：米)随时间ｔ(单位：时)的变化满足函数关系

    h=-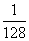(t-19)2+8(0≤t≤40)且当水面到顶点C的距离不大于5米时，需禁止船只通行，请通过计算说明：在这一时段内，需多少小时禁止船只通行？


    (1)依题意有顶点Ｃ的坐标为(0，11)，点Ｂ的坐标为(8，8)，设抛物线解析式为y=ax2+c，有

    解得

    ∴抛物线解析式为y=x2+11.

    (2)令-(t-19)2+8=11-5，解得t1=35，t2=3.

    因为-<0，所以当3≤ｔ≤35时，水面到顶点C的距离不大于5米，需禁止船只通行，禁止船只通行时间为35-3=32(时).

    答：禁止船只通行时间为32小时.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    已知反比例函数y=(m-1) 的图象在第二、四象限，求m的值，并指出在每个象限内y随x的变化情况.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    二次函数y=2x2+mx+8的图象如图所示，则m的值是(     )

      A.-8                B.8                  C.±8                  D.6

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，抛物线y=ax2+bx+c(a＞0)的对称轴是过点(1，0)且平行于y轴的直线，若点P(4，0)在该抛物线上，则4a-2b+c的值为          .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


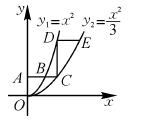
    如图，平行于x轴的直线AC分别交函数y1＝x2(x≥0)与y2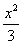＝(x≥0)的图象于B，C两点，过点C作y轴的平行线交y1的图象于点D，直线DE∥AC，交y2的图象于E，则＝          .

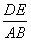    查看答案和解析>>

    科目：初中数学 来源： 题型：


    小磊要制作一个三角形的钢架模型，在这个三角形中，长度为x(单位：cm)的边与这条边上的高之和为40 cm，这个三角形的面积S(单位：cm2)随x(单位：cm)的变化而变化.

    (1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围)；

    (2)当x是多少时，这个三角形面积S最大?最大面积是多少?

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    株洲五桥主桥主孔为拱梁钢构组合体系如图1，小明在五桥观光，发现拱梁的路面部分有均匀排列着9根支柱，他回家上网查到了拱梁是抛物线，其跨度为20米，拱高(中柱)10米，于是他建立如图2的坐标系，将余下的8根支柱的高度都算出来了，你认为中柱右边第二根支柱的高度是(     )

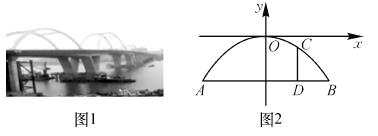
      A.7米                 B.7.6米                 C.8米                D.8.4米

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    将一根长为16π厘米的细铁丝剪成两段,并把每段铁丝围成圆,设所得两圆半径分别为r1和r2.

    (1)求r1与r2的关系式,并写出r1的取值范围;

    (2)将两圆的面积和S表示成r1的函数关系式，求S的最小值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列四个角中，最有可能与70°角互补的是(     )

    查看答案和解析>>

    同步练习册答案