Question

【题目】“面积法”是指利用图形面积间的等量关系寻求线段间等量关系的一种方法．例如：在△ABC中，AB＝AC，点P是BC所在直线上一个动点，过P点作PD⊥AB、PE⊥AC，垂足分别为D、E，BF为腰AC上的高．如图①，当点P在边BC上时，我们可得如下推理：

∵S△ABC＝S△ABP+S△ACP

∴ACBF＝ABPD+ACPE

∵AB＝AC

∴ACBF＝AC（PD+PE）

∴BF＝PD+PE

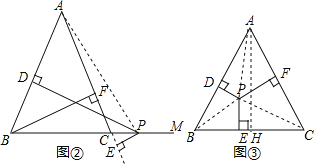
（1）（变式）如图②，在上例的条件下，当点P运动到BC的延长线上时，试探究BF、PD、PE之间的关系，并说明理由．

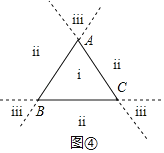
（2）（迁移）如图③，点P是等边△ABC内部一点，作PD⊥AB、PE⊥BC、PF⊥AC，垂足分别为D、E、F，若PD＝1，PE＝2，PF＝4．求△ABC的边长．

（3）（拓展）若点P是等边△ABC所在平面内一点，且点P到三边所在直线的距离分别为2、3、6．请直接写出等边△ABC的高的所有可能

Answer 1

【答案】（1）BF＝PD﹣PE，理由见解析；（2）；（3）11，7，5，1．

【解析】

（1）如图②，连接AP，根据S△ABC＝S△ABP﹣S△ACP列式，即可得到结论；

（2）如图③，过A作AH⊥BC于H，连接PA，PB，PC，根据面积法求出AH＝PD＋PE＋PF＝7，然后根据等边三角形的性质得到CH＝BC＝AC，在Rt△AHC中利用勾股定理构建方程即可得到结论；

（3）如图④，设等边△ABC的高为h，点P到△ABC的三边的距离为h1＝2，h2＝3，h3＝6，分三种情况讨论即可得到结论．

解：（1）BF＝PD﹣PE，

如图②，连接AP，

∵S△ABC＝S△ABP﹣S△ACP，

∴ACBF＝ABPD﹣ACPE，

∵AB＝AC，

∴BF＝PD﹣PE；

（2）如图③，过A作AH⊥BC于H，连接PA，PB，PC，

∵S△ABC＝S△ABP+S△ACP+S△BCP，即AHBC＝PDAB+PFAC+PEBC，

∵△ABC是等边三角形，

∴AB＝AC＝BC，

∴AH＝PD+PE+PF＝7，

∵AB＝AC，AH⊥BC，

∴CH＝BC＝AC，

在Rt△AHC中，∠AHC＝90°，

∴AH2+CH2＝AC2，即49＋AC2＝AC2，

∴AC＝＝；

（3）如图④，设等边△ABC的高为h，点P到△ABC的三边的距离为h1＝2，h2＝3，h3＝6，

当P在i区域时，由（2）可得h＝h1+h2+h3＝2+3+6＝11；

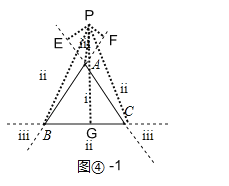
当P在iii区域时，如图④－1，PF＝h1＝2，PE＝h2＝3，PG＝h3＝6，连接

∵S△ABC＝S△PBC－S△ACP－S△ABP＝hBC＝PGBC－PEAC－PFAB，

∵AB＝AC＝BC，

∴h＝h3﹣h2﹣h1＝1，

当P在ii区域时，同理可得h＝h1+h3﹣h2＝2+6﹣3＝5或h＝h2+h3﹣h1＝3+6﹣2＝7，

综上所述，等边△ABC的高的所有可能的值为11，1，7，5．