

分析 (1)根据题意易得点M、P的坐标,利用待定系数法来求直线AB的解析式;
(2设Q(a,a2),由QE∥y轴交AB于E,得到E(a,a+2)于是得到结论;
(3)设M(0,m)解方程组得到A(-1,1),B(2,4),根据两点间的距离公式得到AB2=18,AM2=1+(1-m)2,BM2=4+(4-m)2,然后列方程即可得到结论.
解答 解:(1)如图①,设直线AB与x轴的交点为M.
∵∠OPA=45°,
∴OM=OP=2,即M(-2,0).
设直线AB的解析式为y=kx+b(k≠0),将M(-2,0),P(0,2)两点坐标代入,得$\left\{\begin{array}{l}{2=k×0+b}\\{0=k•(-2)+b}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$.
故直线AB的解析式为y=x+2;
(2)∵点Q在是该抛物线上直线AB的下方的一点,
∴设Q(a,a2),
∵QE∥y轴交AB于E,
∴E(a,a+2)
∴EQ的长度=a+2-a2=-(a-$\frac{1}{2}$)2+$\frac{9}{4}$,
∴EQ的最大值为$\frac{9}{4}$;
(3)设M(0,m)
解$\left\{\begin{array}{l}{y={x}^{2}}\\{y=x+2}\end{array}\right.$得$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{1}=1}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=2}\\{{y}_{2}=4}\end{array}\right.$,
∴A(-1,1),B(2,4),
∴AB2=18,AM2=1+(1-m)2,BM2=4+(4-m)2,
当AB2=AM2+BM2时,
即18=1+(1-m)2+4+(4-m)2,
解得m1=$\frac{5+\sqrt{17}}{2}$,m2=$\frac{5-\sqrt{17}}{2}$,
当AM2=AB2+BM2时,
即1+(1-m)2=18+4+(4-m)2,
解得:m=6,
当BM2=AB2+AM2时,
即4+(4-m)2=18+1+(1-m)2,
解得:m=0,
∴M(0,0),(0,6),(0,$\frac{5+\sqrt{17}}{2}$),(0,$\frac{5-\sqrt{17}}{2}$).
点评 本题考查了二次函数综合题.其中涉及到了待定系数法求一次函数解析式,二次函数图象上点的坐标特征,二次函数的最值的求法,难度比较大.另外,解答(3)题时,一定要分类讨论,做到不重不漏.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
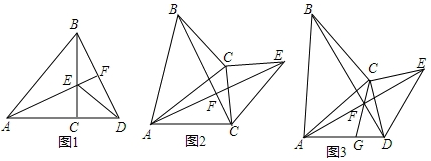
 如图,△ABC在方格纸中,设单元格边长为1.
如图,△ABC在方格纸中,设单元格边长为1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
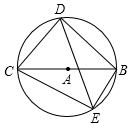 如图,四边形BDCE内接于以BC为直径的⊙A,已知:BC=10,cos∠BCD=$\frac{3}{5}$,∠BCE=30°,则线段DE的长是3+4$\sqrt{3}$.
如图,四边形BDCE内接于以BC为直径的⊙A,已知:BC=10,cos∠BCD=$\frac{3}{5}$,∠BCE=30°,则线段DE的长是3+4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com