
【题目】等腰直角三角形ABC和等腰直角三角形ADE中,∠BAC=∠DAE=90°,AB=4,AE=2,其中△ABC固定,△ADE绕点A作360°旋转,点F、M、N分别为线段BE、BC、CD的中点,连接MN、NF.
问题提出:(1)如图1,当AD在线段AC上时,则∠MNF的度数为 ,线段MN和线段NF的数量关系为 ;
深入讨论:(2)如图2,当AD不在线段AC上时,请求出∠MNF的度数及线段MN和线段NF的数量关系;
拓展延伸:(3)如图3,△ADE持续旋转过程中,若CE与BD交点为P,则△BCP面积的最小值为 .

【答案】(1)45°,NF=![]() MN;(2)∠MNF=45°,NF=
MN;(2)∠MNF=45°,NF=![]() MN;(3)4
MN;(3)4
【解析】
(1)如图1,连接DB,MF,CE,延长BD交EC于H.证明△BAD≌△CAE(SAS),推出BD=EC,∠ACE=∠ABD,再根据三角形中位线定理即可解决问题.
(2)如图2,连接MF,EC,BD.设EC交AB于O,BD交EC于H.证明△BAD≌△CAE(SAS),推出BD=EC,∠ACE=∠ABD,再利用三角形中位线定理即可解决问题.
(3)如图3中,如图3中,如图以A为圆心AD为半径作⊙A.当直线PB与⊙A相切时,△BCP的面积最小.
解:(1)如图1中,连接DB,MF,CE,延长BD交EC于H.
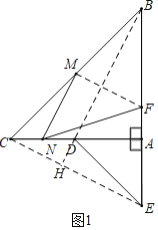
∵AC=AB,AE=AD,∠BAD=∠CAE=90°,
∴△BAD≌△CAE(SAS),
∴BD=CE,∠ACE=∠ABD,
∵∠ABD+∠ADB=90°,∠ADB=∠CDH,
∴∠CDH+∠DCH=90°,
∴∠CHD=90°,
∴EC⊥BH,
∵BM=MC,BF=FE,
∴MF∥EC,MF=![]() EC,
EC,
∵CM=MB,CN=ND,
∴MN∥BD,MN=![]() BD,
BD,
∴MN=MF,MN⊥MF,
∴∠NMF=90°,
∴∠MNF=45°,NF=![]() MN.
MN.
故答案为:45°;NF=![]() MN.
MN.
(2):如图2中,连接MF,EC,BD.设EC交AB于O,BD交EC于H.

∵AC=AB,AE=AD,∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
∴△BAD≌△CAE(SAS),
∴BD=CE,∠ACE=∠ABD,
∵∠AOC+∠ACO=90°,∠AOC=∠BOH,
∴∠OBH+∠BOH=90°,
∴∠BHO=90°,
∴EC⊥BD,
∵BM=MC,BF=FE,
∴MF∥EC,MF=![]() EC,
EC,
∵CM=MB,CN=ND,
∴MN∥BD,MN=![]() BD,
BD,
∴MN=MF,MN⊥MF,
∴∠NMF=90°,
∴∠MNF=45°,NF=![]() MN.
MN.
(3):如图3中,如图以A为圆心AD为半径作⊙A.
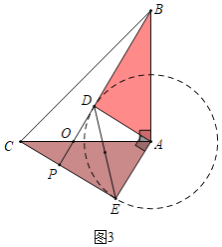
当直线PB与⊙A相切时,此时∠CBP的值最小,点P到BC的距离最小,即△BCP的面积最小,
∵AD=AE,AB=AC,∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠ABD,BD=EC,
∵∠ABD+∠AOB=90°,∠AOB=∠CPO,
∴∠CPB=90°,
∵PB是⊙A的切线,
∴∠ADP=90°,
∵∠DPE=∠ADP=∠DAE=90°,
∴四边形ADPE是矩形,
∵AE=AD,
∴四边形ADPE是正方形,
∴AD=AE=PD=PE=2,BD=EC=![]() =2
=2![]() ,
,
∴PC=2![]() ﹣2,PB=2+2
﹣2,PB=2+2![]() ,
,
∴S△BCP的最小值=![]() ×PC×PB=
×PC×PB=![]() (2
(2![]() ﹣2)(2
﹣2)(2![]() +2)=4.
+2)=4.


科目:初中数学 来源: 题型:
【题目】随着生活水平的提高,人们越来越注重营养健康,有一种有机水果![]() 在市场上特别受欢迎,某大型超市以10元/千克的价格在产地收购了6000千克
在市场上特别受欢迎,某大型超市以10元/千克的价格在产地收购了6000千克![]() 水果,立即将其冷藏,请根据下列信息解决问题:
水果,立即将其冷藏,请根据下列信息解决问题:
①水果![]() 的市场价每天每千克上涨0.1元;
的市场价每天每千克上涨0.1元;
②平均每天有10千克的该水果损坏,不能出售;
③每天的冷藏费用为300元;
④该水果最多保存110天;
(1)若将这批![]() 水果存放
水果存放![]() 天后一次性出售,则
天后一次性出售,则![]() 天后这批水果的销售单价为 元;
天后这批水果的销售单价为 元;
(2)将这批![]() 水果存放多少天后一次性出售所得利润为9600元?
水果存放多少天后一次性出售所得利润为9600元?
(3)将这批![]() 水果存放多少天后一次性出售可获得最大利润?最大利润是多少?
水果存放多少天后一次性出售可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题提出)我们知道:同弧或等弧所对的圆周角都相等,且等于这条弧所对的圆心角的一半.那么,在一个圆内同一条弦所对的圆周角与圆心角之间又有什么关系?
(初步思考)(1)如图,![]() 是
是![]() 的弦,
的弦,![]() ,点
,点![]() 、
、![]() 分别是优弧
分别是优弧![]() 和劣弧
和劣弧![]() 上的点,则
上的点,则![]() ______°.
______°.![]() _______°.
_______°.

(2)如图,![]() 是
是![]() 的弦,圆心角
的弦,圆心角![]() ,点P是
,点P是![]() 上不与A、B重合的一点,求弦
上不与A、B重合的一点,求弦![]() 所对的圆周角
所对的圆周角![]() 的度数(用m的代数式表示).
的度数(用m的代数式表示).

(问题解决)(3)如图,已知线段![]() ,点C在
,点C在![]() 所在直线的上方,且
所在直线的上方,且![]() .用尺规作图的方法作出满足条件的点C所组成的图形(不写作法,保留作图痕迹).
.用尺规作图的方法作出满足条件的点C所组成的图形(不写作法,保留作图痕迹).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了扎实推进精准扶贫工作,某地出台了民生兜底、医保脱贫、教育救助、产业扶持、养老托管和易地搬迁这六种帮扶措施,每户贫困户都享受了2到5种帮扶措施,现把享受了2种、3种、4种和5种帮扶措施的贫困户分别称为A、B、C、D类贫困户.为检査帮扶措施是否落实,随机抽取了若干贫困户进行调查,现将收集的数据绘制成下面两幅不完整的统计图:
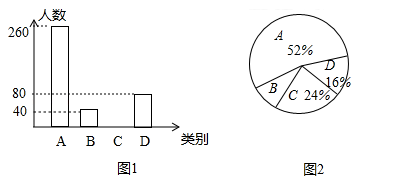
请根据图中信息回答下面的问题:
(1)本次抽样调查了多少户贫困户?
(2)抽查了多少户C类贫困户?并补全统计图;
(3)若该地共有13000户贫困户,请估计至少得到4项帮扶措施的大约有多少户?
(4)为更好地做好精准扶贫工作,现准备从D类贫困户中的甲、乙、丙、丁四户中随机选取两户进行重点帮扶,请用树状图或列表法求出恰好选中甲和丁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△OBF 是直角三角形,∠BFO=90°,∠BOF=30°,△AOB 是等边三角形,OB=4,点 A 与点 F 位于直线 OB 的异侧.
(Ⅰ)如图①,求 BF 及 OF 的长;
(Ⅱ)点 P 是直线OF 上的一个动点,连接 AP,以点 A 为旋转中心,把△AOP 逆时针旋转,使边 AO 与 AB 重合,得△ABD.
①如图②,求在点 P 运动过程中,使点 D 落在线段 OF 上时 OP 的长;
②求在点 P 运动过程中,使点 P 落在线段 OF 上,且△OPD 的面积等于![]() 时 OP 的长(直接写出结果即可).
时 OP 的长(直接写出结果即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是长为10m,倾斜角为30°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).(参考数据:sin65°=0.90,tan65°=2.14)
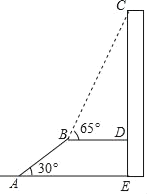
查看答案和解析>>
科目:初中数学 来源: 题型:
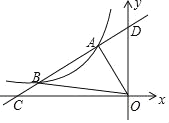
【题目】如图,直线y=kx+b与反比例函数![]() 的图象分别交于点A(﹣1,2),点B(﹣4,n),与x轴,y轴分别交于点C,D.
的图象分别交于点A(﹣1,2),点B(﹣4,n),与x轴,y轴分别交于点C,D.
(1)求此一次函数和反比例函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
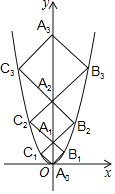
【题目】二次函数y=x2的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…n在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnn都是正方形,则正方形An﹣1BnAnn的周长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com