
【题目】如图,抛物线![]() 与
与![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() ,对称轴交
,对称轴交![]() 轴于点
轴于点![]() .
.
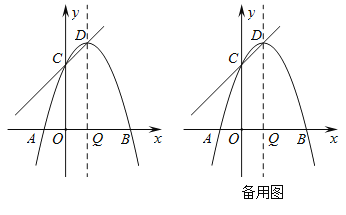
(1)求抛物线的解析式.
(2)若点![]() 是抛物线的对称轴上的一点,以点
是抛物线的对称轴上的一点,以点![]() 为圆心的圆经过
为圆心的圆经过![]() ,
,![]() 两点,且与直线
两点,且与直线![]() 相切,求点
相切,求点![]() 的坐标.
的坐标.
(3)在抛物线的对称轴上是否存在一点![]() ,使得
,使得![]() 与
与![]() 相似?如果存在,求出点
相似?如果存在,求出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
【答案】(1)![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() 或
或![]() ;(3)存在,点
;(3)存在,点![]() 的坐标为
的坐标为![]() 或
或![]()
【解析】
(1)由题意把点A、点B的坐标代入抛物线解析式,用待定系数法可得到二次函数的表达式;
(2)根据题意设直线CD切⊙P于点E.连结PE、PA,作CF⊥DQ于点F.通过DF与CF的长,说明△DCF为等腰直角三角形.设点P(1,m),用含m的代数式表示出半径EP、PA的长,根据半径间关系,求出m的值从而确定点P的坐标.
(3)根据题意利用等腰直角三角形,先求出DC和BC的长,由于∠CBQ=∠CDM,若△DCM与△BQC相似,分两种情况,利用比例线段求出满足条件的点M的坐标即可.
解:(1)∵![]() ,
,![]() 在抛物线上,
在抛物线上,
代入![]() ,得
,得![]() ,
,
解得![]()
∴抛物线的解析式为![]() .
.
(2)如图1,设直线![]() 切
切![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,作
,作![]() 于点
于点![]() .
.
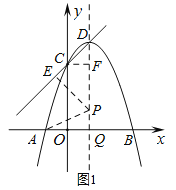
∴![]()
![]() .
.
由![]() ,得对称轴为直线
,得对称轴为直线![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 为等腰直角三角形.
为等腰直角三角形.
设![]() ,则
,则![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() .
.
整理,得![]() ,
,
解得![]() .
.
∴点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
(3)存在点![]() ,使得
,使得![]() .
.
如图2,连接![]() ,
,![]() ,
,![]() ,
,
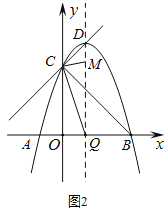
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,![]() .
.
由(2)可知,![]() ,
,![]()
∴![]() .
.
∴![]() 与
与![]() 相似有两种情况,
相似有两种情况,
当![]() 时,
时,![]() ,解得
,解得![]() ,
,
∴![]() .
.
∴![]()
当![]() 时,
时,![]() ,解得
,解得![]() ,
,
∴![]() ,
,
∴![]() .
.
综上,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】随着某市养老机构(养老机构指社会福利院、养老院、社区养老中心等)建设稳步推进,拥有的养老床位及养老建筑不断增加.
(1)该市的养老床位数从2017年底的2万个增长到2019年底的2.88万个,求该市这两年(从2017年底到2019年底)拥有的养老床位数的平均年增长率;
(2)该市某社区今年准备新建一养老中心,如果计划赡养200名老人,建筑投入平均5万元/人,且计划赡养的老人每增加5人,建筑投入平均减少1000元/人,那么新建该养老中心需申报的最高建筑投入是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转90°得到线段
顺时针旋转90°得到线段![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .
.

(1)求直线![]() 和反比例函数
和反比例函数![]() 的解析式;
的解析式;
(2)已知点![]() 是反比例函数
是反比例函数![]() 图象上的一个动点,求点
图象上的一个动点,求点![]() 到直线
到直线![]() 距离最短时的坐标.
距离最短时的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
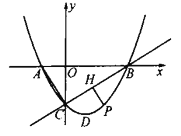
【题目】已知在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),与
左侧),与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() .
.
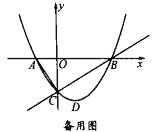
(1)如图,直线![]() 下方抛物线上的一个动点
下方抛物线上的一个动点![]() (不与点
(不与点![]() 重合),过点
重合),过点![]() 作
作![]() 于点
于点![]() ,当
,当![]() 最大时,点
最大时,点![]() 为线段
为线段![]() 一点(不与点
一点(不与点![]() 重合),当
重合),当![]() 的值最小时,求点
的值最小时,求点![]() 的坐标;
的坐标;
(2)将![]() 沿直线
沿直线![]() 翻折得
翻折得![]() ,再将
,再将![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() 得
得![]() ,在旋转过程中直线
,在旋转过程中直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,当
,当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知小正方形ABCD的面积为1,把它的各边延长一倍得到新正方形A1B1C1D1;把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2(如图(2));正方形A2B2C2D2的面积为________,以此下去…,则正方形AnBnCnDn的面积为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,将
,将![]() 绕点
绕点![]() 按逆时针方向旋转,得到
按逆时针方向旋转,得到![]() .
.
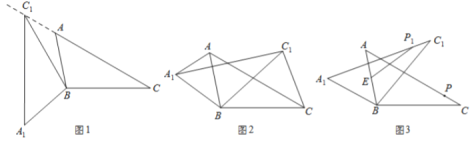
(1)如图 1,当点![]() 在线段
在线段![]() 的延长线上时,求
的延长线上时,求![]() 的度数;
的度数;
(2)如图 2,连接![]() ,
,![]() .若
.若![]() 的面积为 3,求
的面积为 3,求![]() 的面积;
的面积;
(3)如图 3,点![]() 为线段
为线段![]() 中点,点
中点,点![]() 是线段
是线段![]() 上的动点,在
上的动点,在![]() 绕点
绕点![]() 按逆时针方向旋转的过程中,点
按逆时针方向旋转的过程中,点![]() 的对应点是点
的对应点是点![]() ,求线段
,求线段![]() 长度的最大值与最小值.
长度的最大值与最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:数学课上,老师出示了这样一个问题:
如图1,在等边![]() 中,点
中,点![]() 、
、![]() 在
在![]() 上,且
上,且![]() ,直线
,直线![]() 交
交![]() 于
于![]() 点,交
点,交![]() 延长线于
延长线于![]() 点,且
点,且![]() ,探究线段
,探究线段![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
某学习小组的同学经过思考,交流了自己的想法:
小明:“通过观察和度量,发现![]() 与
与![]() 存在某种数量关系”;
存在某种数量关系”;
小强:“通过观察和度量,发现图1中有一条线段与![]() 相等”;
相等”;
小伟:“通过构造三角形,证明三角形全等,进而可以得到线段![]() 之间的数量关系”.
之间的数量关系”.
……
老师:“保留原题条件,再过点![]() 作
作![]() 交
交![]() 于
于![]() 与
与![]() 相交于点
相交于点![]() (如图2)如果给出
(如图2)如果给出![]() 的值,那么可以求出
的值,那么可以求出![]() 的值”.
的值”.
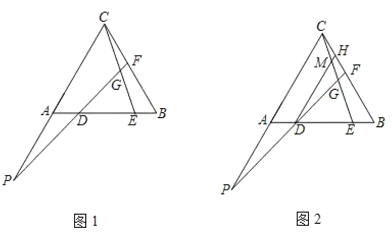
请回答:
(1)在图1中找出![]() 与
与![]() 数量关系,并证明;
数量关系,并证明;
(2)在图1中找出与线段![]() 相等的线段,并证明;
相等的线段,并证明;
(3)探究线段![]() 之间的数量关系,并证明;
之间的数量关系,并证明;
(4)若![]() ,求
,求![]() 的值(用含
的值(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 为
为![]() 上一动点,
上一动点,![]() 点从
点从![]() 点以1个单位/秒的速度向
点以1个单位/秒的速度向![]() 点运动,远动到
点运动,远动到![]() 点即停止,经过
点即停止,经过![]() 点作
点作![]() ,交
,交![]() 于点
于点![]() ,以
,以![]() 为一边在
为一边在![]() 一侧作正方形
一侧作正方形![]() ,在
,在![]() 点运动过程中,设正方形
点运动过程中,设正方形![]() 与
与![]() 的重叠面积为
的重叠面积为![]() ,运动时间为
,运动时间为![]() 秒,如图2是
秒,如图2是![]() 与
与![]() 的函数图象.
的函数图象.
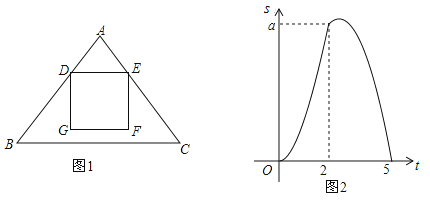
(1)求![]() 的长;
的长;
(2)求![]() 的值;
的值;
(3)求![]() 与
与![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com