
【题目】如图,矩形ABCD中,AB=2,将矩形ABCD绕点D逆时针旋转90°,点A、C分别落在点A′、C′处,如果点A′、C′、B在同一条直线上,则∠CBA′的正切值为___.

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】在信息技术飞速发展的今天,智能手机的使用呈现出低龄化的趋势,中小学生使用智能手机成为十分普遍的现象,但智能手机给生活带来便利的同时,也对中小学生的身心发展带来一些不利影响,比如手机屏幕对视力的伤害、关注各种“垃圾新闻”对时间的浪费、沉迷手机游戏缺少运动、人际交往等等,这些现象引起了家长、学校、社会的广泛关注.对此,成都某中学学生会发出了“中小学生使用非智能手机”的倡议,鼓励同学们全面发展,追逐梦想,把更多时间用在将来能够成就自我的地方.据统计,今年9月该中学使用非智能手机的同学有128人,倡议发出后,11月使用非智能手机的同学上升到了200人.
(1)若从9月到11月使用非智能手机的同学平均增长率相同,那么按此增长率增长到12月份该校使用非智能手机的同学将有多少人?
(2)某于机制造商发现当下市场上售卖的非智能手机大多品质不佳、外观设计成就,难以满足市场的需要,所以该厂决定投入12万元全部用于生产![]() 型、
型、![]() 型两款精美的“学生专用手机”投入市场,一部
型两款精美的“学生专用手机”投入市场,一部![]() 型手机生产成本为400元,售价为600元;一部
型手机生产成本为400元,售价为600元;一部![]() 型手机生产成本为600元,售价为930元,该厂计划生产
型手机生产成本为600元,售价为930元,该厂计划生产![]() 型手机的数量不少于
型手机的数量不少于![]() 型手机数量的2倍,但不超过
型手机数量的2倍,但不超过![]() 型手机数量的2.3倍,求生产这批手机并全部售卖后可获得的最大利润.
型手机数量的2.3倍,求生产这批手机并全部售卖后可获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
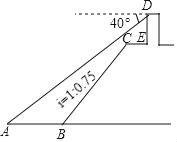
【题目】如图,小王在长江边某瞭望台D处测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为多少米?(结果精确到0.1,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
查看答案和解析>>
科目:初中数学 来源: 题型:
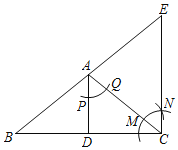
【题目】如图,在△ABC中,AD为边BC上的中线,且AD平分∠BAC.嘉淇同学先是以A为圆心,任意长为半径画弧,交AD于点P,交AC于点Q,然后以点C为圆心,AP长为半径画弧,交AC于点M,再以M为圆心,PQ长为半径画弧,交前弧于点N,作射线CN,交BA的延长线于点E.
(1)通过嘉淇的作图方法判断AD与CE的位置关系是 ,数量关系是 ;
(2)求证:AB=AC;
(3)若BC=24,CE=10,求△ABC的内心到BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽是4 m.按照图中所示的直角坐标系,抛物线可以用y=![]() x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为
x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为![]() m.
m.
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系xOy中,点A的坐标为(9,6),AB⊥y轴,垂足为B,点P从原点O出发向x轴正方向运动,同时,点Q从点A出发向点B运动,当点Q到达点B时,点P、Q同时停止运动,若点P与点Q的速度之比为1:2,则下列说法正确的是( )
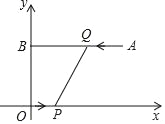
A. 线段PQ始终经过点(2,3)
B. 线段PQ始终经过点(3,2)
C. 线段PQ始终经过点(2,2)
D. 线段PQ不可能始终经过某一定点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线过O、A、B三点,A(4,0)B(1,-3),P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q.
(1)直线PQ与x轴所夹锐角的度数,并求出抛物线的解析式.
(2)当点P在x轴下方的抛物线上时,过点C(2,2)的直线AC与直线PQ交于点D,求: PD+DQ的最大值;②PD.DQ的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
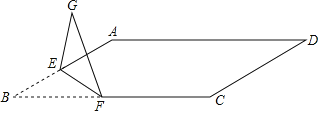
【题目】如图,在ABCD中,AB=6,BC=6![]() ,∠D=30°,点E是AB边的中点,点F是BC边上一动点,将△BEF移沿直线EF折叠,得到△GEF,当FG∥AC时,BF的长为_____.
,∠D=30°,点E是AB边的中点,点F是BC边上一动点,将△BEF移沿直线EF折叠,得到△GEF,当FG∥AC时,BF的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com