
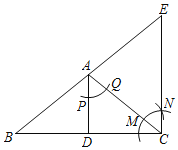
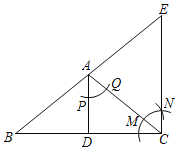
【题目】如图,在△ABC中,AD为边BC上的中线,且AD平分∠BAC.嘉淇同学先是以A为圆心,任意长为半径画弧,交AD于点P,交AC于点Q,然后以点C为圆心,AP长为半径画弧,交AC于点M,再以M为圆心,PQ长为半径画弧,交前弧于点N,作射线CN,交BA的延长线于点E.
(1)通过嘉淇的作图方法判断AD与CE的位置关系是 ,数量关系是 ;
(2)求证:AB=AC;
(3)若BC=24,CE=10,求△ABC的内心到BC的距离.
【答案】(1)AD∥CE,EC=2AD;(2)见解析;(3)r=![]() .
.
【解析】
(1)由作图方法可知∠DAC=∠ACE,则AD∥CE,根据BC=2BD,可证CE=2AD;
(2)由(1)知△ABD∽△EBC,证出BE=2AB,得AB=AE,又AC=AE,则AB=AC;
(3)设△ABC内心到BC距离为r,可得![]() ,即可求出r.
,即可求出r.
(1)∵嘉淇的作图方法可知∠DAC=∠ACE,
∴AD∥CE,
∴△ABD∽△EBC,
∴![]() ,
,
∵AD为边BC上的中线,
∴BC=2BD,
∴CE=2AD,
故答案为:AD∥CE,EC=2AD;
(2)证明:∵AD∥CE,
∴∠BAD=∠E,∠DAC=∠ACE,
∵AD平分∠BAC,
∴∠BAD=∠DAC,
∴∠ACE=∠E,
∴AC=AE,
由(1)知△ABD∽△EBC,
∴![]() ,
,
∴EB=2AB,即AB=AE,
∴AB=AC.
(3)解:∵BC=24,CE=10,
∴BD=12,AD=5,
∵AB=AC,BD=CD,
∴AD⊥BD,
设△ABC内心到BC距离为r,
∴![]() ,
,
∴![]() ,
,
∴60﹣12r=13r
∴25r=60,
∴r=![]() .
.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
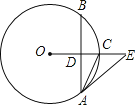
【题目】如图,在⊙O中,半径OC垂直于弦AB,垂足为点D,点E在OC的延长线上,∠EAC=∠BAC
(1)求证:AE是⊙O的切线;
(2)若AB=8,cosE=![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
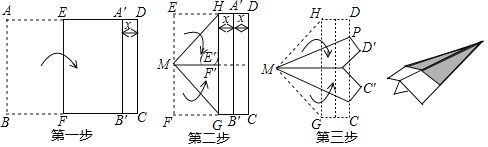
【题目】折纸飞机是我们儿时快乐的回忆,现有一张长为290mm,宽为200mm的白纸,如图所示,以下面几个步骤折出纸飞机:(说明:第一步:白纸沿着EF折叠,AB边的对应边A′B′与边CD平行,将它们的距离记为x;第二步:将EM,MF分别沿着MH,MG折叠,使EM与MF重合,从而获得边HG与A′B′的距离也为x),则PD=______mm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接2011年高中招生考试,某中学对全校九年级学生进行了一次数学摸底考试,并随机抽取了部分学生的测试成绩作为样本进行,绘制成了如下两幅不完整的统计图,请根据图中所给信息,下列问题:
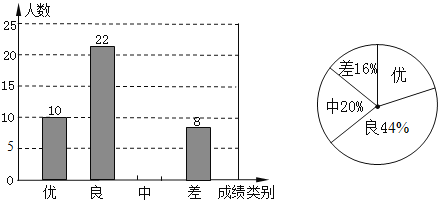
(1)请将表示成绩类别为“中”的条形统计图补充完整;
(2)在扇形统计图中,表示成绩类别为“优”的扇形所对应的圆心角是 72 度;
(3)学校九年级共有1000人参加了这次数学考试,估算该校九年级共有多少名学生的数学成绩可以达到优秀?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于点D,C在BD上,有四位同学分别测量出以下四组数据:①BC,∠ACB;②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A、B间距离的有( )
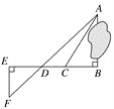
A. 4组B. 3组C. 2组D. 1组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初二年級教师对试卷讲评课中学生参与的深度与广度进行评价调査,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初二学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:
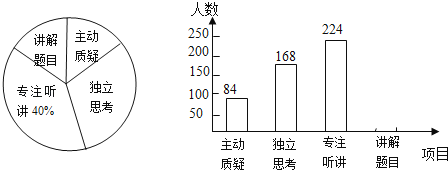
(1)在这次评价中,一共抽査了 名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为 度;
(3)请将频数分布直方图补充完整:
(4)如果全市有30000名初二学生,那么在试卷评讲课中,请估计“独立思考”的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动中,小明发现将两块不同的等腰直角三角板进行旋转,能得到一组结论:在其中一块三角板Rt△ABC,AB=BC=4,∠B为直角,将另一块等腰直角三角板的直角顶点放在斜边AC的中点O处,将三角板绕点O旋转,三角板的两直角边分别交AB、BC或其延长线于E、F两点,如图①与②是旋转三角板所得图形的两种情况.
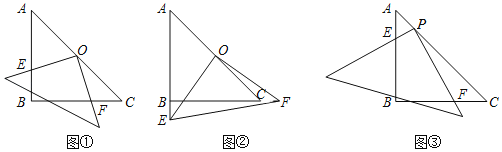
(1)三角板绕点O旋转,△OFC是否能成为等腰直角三角形?若能,求出CF;若不能,请说明理由;
(2)三角板绕点O旋转,线段OE和OF之间有什么数量关系?用图②加以证明;
(3)若将三角板的直角原点放在斜边上的点P处(如图③),当![]() ,PF和PE有怎样的数量关系,证明你发现的结论.
,PF和PE有怎样的数量关系,证明你发现的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2018年“新技术支持未来教育”的教师培训活动中,会议就“面向未来的学校教育、家庭教育及实践应用演示”等问题进行了互动交流,记者随机采访了部分参会教师,对他们发言的次数进行了统计,并绘制了不完整的统计表和条形统计图.
组别 | 发言次数n | 百分比 |
A | 0≤n<3 | 10% |
B | 3≤n<6 | 20% |
C | 6≤n<9 | 25% |
D | 9≤n<12 | 30% |
E | 12≤n<15 | 10% |
F | 15≤n<18 | m% |
请你根据所给的相关信息,解答下列问题:
(1)本次共随机采访了 _____ 名教师,m= _____ ;
(2)补全条形统计图;
(3)已知受访的教师中,E组只有2名女教师,F组恰有1名男教师,现要从E组、F组中分别选派1名教师写总结报告,请用列表法或画树状图的方法,求所选派的两名教师恰好是1男1女的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com