
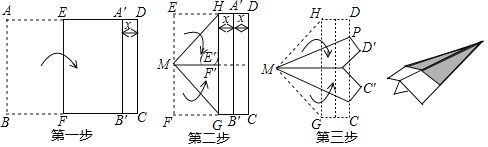
【题目】折纸飞机是我们儿时快乐的回忆,现有一张长为290mm,宽为200mm的白纸,如图所示,以下面几个步骤折出纸飞机:(说明:第一步:白纸沿着EF折叠,AB边的对应边A′B′与边CD平行,将它们的距离记为x;第二步:将EM,MF分别沿着MH,MG折叠,使EM与MF重合,从而获得边HG与A′B′的距离也为x),则PD=______mm.
【答案】![]()
【解析】
延长ME′交CD于T,在TM上截取TW=TP,设DP=m.构建方程可求得x=30,TW=TP可知∠PWT=45°,∠PMW=22.5°,进而∠WMP=∠WPM=22.5°,可求得MW=PW=![]() (100-m)可构建方程
(100-m)可构建方程![]() (100-m)+100-m=16,解得m=(260-160
(100-m)+100-m=16,解得m=(260-160![]() )mm,即可解决问题.
)mm,即可解决问题.
解:延长ME′交CD于T,在TM上截取TW=TP,设DP=m.
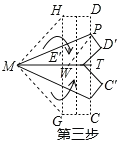
由题意MW=WM=100,MT=160
3x=290-200
x=30
∵TW=TP
∴∠PWT=45°
∵∠PWT=∠PMT+∠MPW,∠PMW=22.5°
∴∠WMP=∠WPM=22.5°
∴MW=PW=![]() (100-m)
(100-m)
∴![]() (100-m)+100-m=160
(100-m)+100-m=160
解得m=(260-160![]() )mm
)mm
∴PD=(260-160![]() )mm
)mm
故答案为260-160![]()


科目:初中数学 来源: 题型:
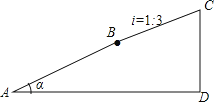
【题目】小林从点A出发,沿着坡角为α的斜坡向上走了650米到达点B,且sinα=![]() .然后又沿着坡度i=1:3的斜坡向上走了500米达到点C.
.然后又沿着坡度i=1:3的斜坡向上走了500米达到点C.
(1)小明从A点到B点上升的高度是多少米?
(2)小明从A点到C点上升的高度CD是多少米?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
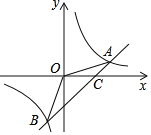
【题目】如图,一次函数y=x﹣2的图象与反比例函数y=![]() (k>0)的图象相交于A、B两点,与x轴交于点C,连接OA、OB,且tan∠AOC=
(k>0)的图象相交于A、B两点,与x轴交于点C,连接OA、OB,且tan∠AOC=![]() .
.
(1)求反比例函数的解析式;
(2)D是y轴上一点,且△BOD是以OB为腰的等腰三角形,请你求出所有符合条件的D点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四个命题:①如果一个数的相反数等于它本身,则这个数是0;②一个数的倒数等于它本身,则这个数是1;③一个数的算术平方根等于它本身,则这个数是1或0;④甲、乙两射击运动员分别射击10次,他们射击成绩的方差分别为![]() =5,
=5,![]() =2,这一过程中乙发挥比甲更稳定.⑤点M(a,b),N(c,d)都在反比例函数y=
=2,这一过程中乙发挥比甲更稳定.⑤点M(a,b),N(c,d)都在反比例函数y=![]() 的图象上.若a<c,则b>d.其中真命题有( )个.
的图象上.若a<c,则b>d.其中真命题有( )个.
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解
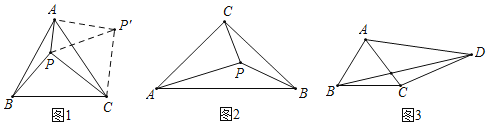
利用旋转变换解决数学问题是一种常用的方法.如图1,点P是等边三角形ABC内一点,PA=1,PB=![]() ,PC=2.求∠BPC的度数.
,PC=2.求∠BPC的度数.
为利用已知条件,不妨把△BPC绕点C顺时针旋转60°得△AP′C,连接PP′,则PP′的长为_____;在△PAP′中,易证∠PAP′=90°,且∠PP′A的度数为_____,综上可得∠BPC的度数为_____;
(2)类比迁移
如图2,点P是等腰Rt△ABC内的一点,∠ACB=90°,PA=2,PB=![]() ,PC=1,求∠APC的度数;
,PC=1,求∠APC的度数;
(3)拓展应用
如图3,在四边形ABCD中,BC=3,CD=5,AB=AC=![]() AD.∠BAC=2∠ADC,请直接写出BD的长.
AD.∠BAC=2∠ADC,请直接写出BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级甲、乙两班各有学生50人,为了了解这两个班学生身体素质情况,进行了抽样调查,过程如下,请补充完整.
(1)收集数据:从甲、乙两个班各随机抽取10名学生进行身体素质测试,测试成绩(百分制)如下:
甲班65 75 75 80 60 50 75 90 85 65
乙班90 55 80 70 55 70 95 80 65 70
(2)整理描述数据:按如下分数段整理、描述这两组样本数据:
成绩x 人数 班级 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
甲班 | 1 | 3 | 3 | 2 | 1 |
乙班 | 2 | 1 | m | 2 | n |
在表中:m=______,n=______.
(3)分析数据:
①两组样本数据的平均数、中位数、众数如表所示:
班级 | 平均数 | 中位数 | 众数 |
甲班 | 72 | x | 75 |
乙班 | 72 | 70 | y |
在表中:x=______,y=______.
②若规定测试成绩在80分(含80分)以上的学生身体素质为优秀,请估计乙班50名学生中身体素质为优秀的学生有______人.
③现从甲班指定的2名学生(1男1女),乙班指定的3名学生(2男1女)中分别抽取1名学生去参加上级部门组织的身体素质测试,用树状图和列表法求抽到的2名同学是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)尝试探究
如图1,等腰Rt△ABC的两个顶点B,C在直线MN上,点D是直线MN上一个动点(点D在点C的右边),BC=3,BD=m,在△ABC同侧作等腰Rt△ADE,∠ABC=∠ADE=90°,EF⊥ MN于点F,连结CE.
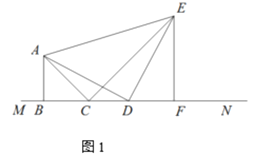
①求DF的长;
②在判断AC⊥CE是否成立时,小明同学发现可以由以下两种思路解决此问题:
思路一:先证CF=EF,求出∠ECF=45°,从而证得结论成立.
思路二:先求DF,EF的长,再求CF的长,然后证AC2+CE2=AE2,从而证得结论成立.
请你任选一种思路,完整地书写本小题的证明过程.(如用两种方法作答,则以第一种方法评分)
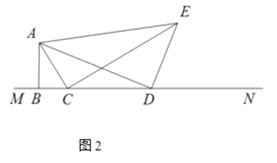
(2)拓展探究
将(1)中的两个等腰直角三角形都改为有一个角为的直角三角形,如图2, ∠ABC=∠ADE=90°,∠BAC=∠DAE=30°,BC=3,BD=m,当4≤m≤6时,求CE长的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.
(1)当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;
(2)在(1)的条件下,若DE:AE:CE= 1: ![]() :3,求∠AED的度数;
:3,求∠AED的度数;
(3)若BC= 4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的一边DF与边DM重合时(如图2),若OF=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级共有80名同学参与数学科托底训练.其中(1)班30人,(2)班25人,(3)班25人,吕老师在托底训练后对这些同学进行测试,并对测试成绩进行整理,得到下面统计图表.
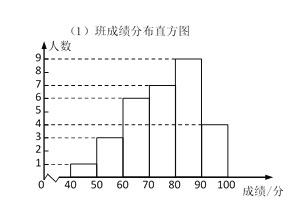
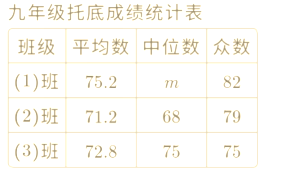
(1)表格中的m落在________组;(填序号)
①40≤x<50, ②50≤x<60, ③60≤x<70,
④70≤x<80, ⑤80≤x<90, ⑥90≤x≤100.
(2)求这80名同学的平均成绩;
(3)在本次测试中,(2)班小颖同学的成绩是70分,(3)班小榕同学的成绩是74分,这两位同学成绩在自己所在班级托底同学中的排名,谁更靠前?请简要说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com