
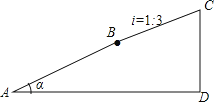
【题目】小林从点A出发,沿着坡角为α的斜坡向上走了650米到达点B,且sinα=![]() .然后又沿着坡度i=1:3的斜坡向上走了500米达到点C.
.然后又沿着坡度i=1:3的斜坡向上走了500米达到点C.
(1)小明从A点到B点上升的高度是多少米?
(2)小明从A点到C点上升的高度CD是多少米?(结果保留根号)
【答案】(1)小明从A点到点B上升的高度是200米;(2)点C相对于起点A升高了(50![]() +200)米.
+200)米.
【解析】
(1)根据题意画出图形,进而利用锐角三角函数关系求出BF;
(2)利用坡度的定义求得CE的长,即可得出点C相对于起点A升高的高度.
解:(1)如图所示:过点B作BF⊥AD于点F,BE⊥CD于点E,过点C作CD⊥AD于点D,
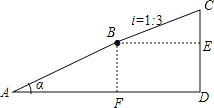
由题意得:AB=650米,BC=500米,
∴sinα=![]() =
=![]() =
=![]() ,
,
∴BF=650×![]() =200米,
=200米,
∴小明从A点到点B上升的高度是200米;
(2)∵斜坡BC的坡度为:1:3,
∴CE:BE=1:3,
设CE=x,则BE=3x,
由勾股定理得:x2+(3x)2=5002
解得:x=50![]() ,
,
∴CD=CE+DE=BF+CE=200+50![]() ,
,
答:点C相对于起点A升高了(50![]() +200)米.
+200)米.
故答案为:(1)小明从A点到点B上升的高度是200米;(2)点C相对于起点A升高了(50![]() +200)米.
+200)米.


科目:初中数学 来源: 题型:
【题目】如图所示,![]() 城市在
城市在![]() 城市正东方向,现计划在
城市正东方向,现计划在![]() ,
,![]() 两城市间修建一条高速公路(即线段
两城市间修建一条高速公路(即线段![]() ).经测量,森林保护区的中心
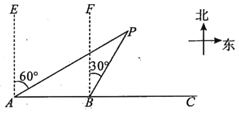
).经测量,森林保护区的中心![]() 在城市
在城市![]() 的北偏东
的北偏东![]() 方向上,在线段
方向上,在线段![]() 上距
上距![]() 城市
城市![]() 的
的![]() 处测得
处测得![]() 在北偏东
在北偏东![]() 方向上,已知森林保护区是以点
方向上,已知森林保护区是以点![]() 为圆心,
为圆心,![]() 为半径的圆形区域.这条高速铁路是否会穿越保护区?请通过计算说明.(参考数据:
为半径的圆形区域.这条高速铁路是否会穿越保护区?请通过计算说明.(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为直径作圆,交斜边AB于点E,D为AC的中点.连接DO,DE.则下列结论中不一定正确的是( )

A. DO∥ABB. △ADE是等腰三角形
C. DE⊥ACD. DE是⊙O的切线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若平面直角坐标系内的点M满足横、纵坐标都为整数,则把点M叫做“整点”.例如:P(1,0)、Q(2,﹣2)都是“整点”.抛物线y=mx2﹣4mx+4m-2(m![]() 0)与x轴交于点A、B两点,若该抛物线在A、B之间的部分与线段AB所围成的区域(包括边界)恰有七个整点,则m的取值范围是( )
0)与x轴交于点A、B两点,若该抛物线在A、B之间的部分与线段AB所围成的区域(包括边界)恰有七个整点,则m的取值范围是( )
A. ![]() <m≤1B.
<m≤1B. ![]() ≤m<1C. 1<m≤2D. 1<m<2
≤m<1C. 1<m≤2D. 1<m<2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知点![]() 的坐标为
的坐标为![]() .
.
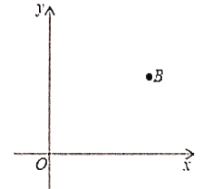
(1)请用直尺(不带刻度)和圆规作一条直线![]() ,它与
,它与![]() 轴和
轴和![]() 轴的正半轴分别交于点
轴的正半轴分别交于点![]() 和点
和点![]() ,且
,且![]() 与
与![]() 关于直线
关于直线![]() 对称.(作图不必写作法,但要保留作图痕迹.)
对称.(作图不必写作法,但要保留作图痕迹.)
(2)请求出(1)中作出的直线![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
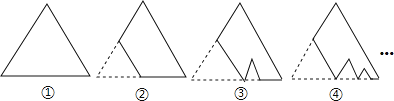
【题目】如图,图①是一块边长为1,周长记为P1的等边三角形纸板,沿图①的底边剪去一块边长的![]() 的等边三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的
的等边三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的![]() )后,得图③,④,…,记第n(n≥3)块纸板的周长为Pn,则Pn-Pn-1=_________
)后,得图③,④,…,记第n(n≥3)块纸板的周长为Pn,则Pn-Pn-1=_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]()
![]() 对称轴为______,顶点坐标为______;
对称轴为______,顶点坐标为______;
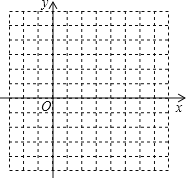
![]() 在坐标系中利用五点法画出此抛物线.
在坐标系中利用五点法画出此抛物线.
x |
| ______ | ______ | ______ | ______ | ______ |
|
y |
| ______ | ______ | ______ | ______ | ______ |
|
![]() 若抛物线与x轴交点为A、B,点
若抛物线与x轴交点为A、B,点![]() 在抛物线上,求
在抛物线上,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
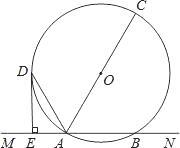
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com