
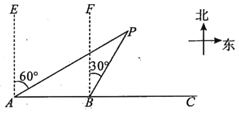
【题目】如图所示,![]() 城市在
城市在![]() 城市正东方向,现计划在
城市正东方向,现计划在![]() ,
,![]() 两城市间修建一条高速公路(即线段
两城市间修建一条高速公路(即线段![]() ).经测量,森林保护区的中心
).经测量,森林保护区的中心![]() 在城市
在城市![]() 的北偏东
的北偏东![]() 方向上,在线段
方向上,在线段![]() 上距
上距![]() 城市
城市![]() 的
的![]() 处测得
处测得![]() 在北偏东
在北偏东![]() 方向上,已知森林保护区是以点
方向上,已知森林保护区是以点![]() 为圆心,
为圆心,![]() 为半径的圆形区域.这条高速铁路是否会穿越保护区?请通过计算说明.(参考数据:
为半径的圆形区域.这条高速铁路是否会穿越保护区?请通过计算说明.(参考数据:![]() )
)
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
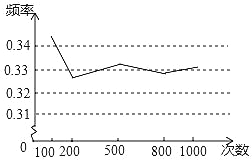
【题目】某学习小组做“用频率估计概率的试验时,统计了某一结果出现的频率,绘制了如图所示折线统计图,则符合这一结果的试验最有可能的是( )
A. 掷一枚正六面体的骰子,出现1点朝上
B. 任意写一个整数,它能被2整除
C. 不透明袋中装有大小和质地都相同的1个红球和2个黄球,从中随机取一个,取到红球
D. 先后两次掷一枚质地均匀的硬币,两次都出现反面
查看答案和解析>>
科目:初中数学 来源: 题型:
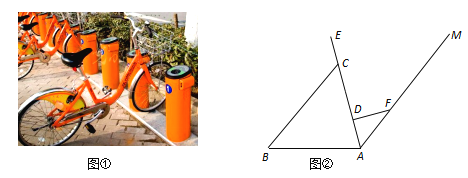
【题目】“低碳环保,你我同行”.近几年,各大城市的公共自行车给市民出行带来了极大的方便.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A.D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,⊙O过正方形ABCD的顶点A、D且与边BC相切于点E,分别交AB、DC于点M、N.动点P在⊙O或正方形ABCD的边上以每秒一个单位的速度做连续匀速运动.设运动的时间为x,圆心O与P点的距离为y,图2记录了一段时间里y与x的函数关系,在这段时间里P点的运动路径为( )

A. 从D点出发,沿弧DA→弧AM→线段BM→线段BC
B. 从B点出发,沿线段BC→线段CN→弧ND→弧DA
C. 从A点出发,沿弧AM→线段BM→线段BC→线段CN
D. 从C点出发,沿线段CN→弧ND→弧DA→线段AB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°
(1)如图①,若∠ACD=60°,BC=1,CD=3,则AC的长为 ;
(2)如图②,若∠ACD=45°,BC=1,CD=3,求出AC的长;
(3)如图③,若∠ACD=30°,BC=a,CD=b,直接写出AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,已知
中,已知![]() ,在边
,在边![]() 上取点
上取点![]() ,使
,使![]() ,连结
,连结![]() ,过点
,过点![]() 作
作![]() ,与边
,与边![]() 或其延长线交于点
或其延长线交于点![]() .
.
猜想:如图①,当点![]() 在边
在边![]() 上时,线段
上时,线段![]() 与
与![]() 的大小关系为 .
的大小关系为 .
探究:如图②,当点![]() 在边
在边![]() 的延长线上时,
的延长线上时,![]() 与边
与边![]() 交于点
交于点![]() .判断线段
.判断线段![]() 与
与![]() 的大小关系,并加以证明.
的大小关系,并加以证明.
应用:如图②,若![]() 利用探究得到的结论,求线段
利用探究得到的结论,求线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
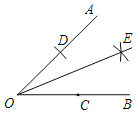
【题目】如图是小西设计的“作已知角∠AOB的平分线”的尺规作图过程:
①在射线OB上取一点C;
②以点O为圆心,OC长为半径作弧,交射线OA于点D;
③分别以点C,D为圆心,OC长为半径作弧,两弧相交于点E;
④作射线OE.
则射线OE即为∠AOB的角平分线.
请观察图形回答下列问题:
(1)由步骤②知,线段OC,OD的数量关系是______;连接DE,CE,线段CO,CE的数量关系是______;
(2)在(1)的条件下,若∠EOC=25°,求∠ECB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
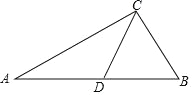
【题目】如图,在△ABC中,CD是边AB上的中线,∠B是锐角,sinB=![]() ,tanA=
,tanA=![]() ,AC=
,AC=![]() ,
,
(1)求∠B 的度数和 AB 的长.
(2)求 tan∠CDB 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
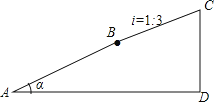
【题目】小林从点A出发,沿着坡角为α的斜坡向上走了650米到达点B,且sinα=![]() .然后又沿着坡度i=1:3的斜坡向上走了500米达到点C.
.然后又沿着坡度i=1:3的斜坡向上走了500米达到点C.
(1)小明从A点到B点上升的高度是多少米?
(2)小明从A点到C点上升的高度CD是多少米?(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com