
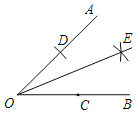
【题目】如图是小西设计的“作已知角∠AOB的平分线”的尺规作图过程:
①在射线OB上取一点C;
②以点O为圆心,OC长为半径作弧,交射线OA于点D;
③分别以点C,D为圆心,OC长为半径作弧,两弧相交于点E;
④作射线OE.
则射线OE即为∠AOB的角平分线.
请观察图形回答下列问题:
(1)由步骤②知,线段OC,OD的数量关系是______;连接DE,CE,线段CO,CE的数量关系是______;
(2)在(1)的条件下,若∠EOC=25°,求∠ECB的度数.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
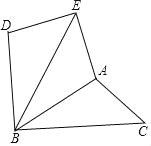
【题目】如图所示,∠DBC=90°,∠C=45°,AC=2,△ABC绕点B逆时针旋转60°得到△DBE,连接AE.
(1)求证:△ABC≌△ABE;
(2)连接AD,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
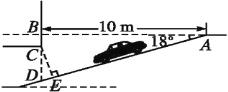
【题目】.某商场为缓解“停车难”问题,拟建造地下停车库,如图是该地下停车库坡道入口的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5 m.根据规定,地下停车库坡道入口上方要张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.小明认为CD的长就是所限制的高度,而小亮认为应该以CE的长作为限制的高度.小明和小亮谁说得对?请你判断并计算出正确的结果.(结果精确到0.1 m,参考数据:sin 18°≈0.31,cos 18°≈0.95,tan 18°≈0.325)
查看答案和解析>>
科目:初中数学 来源: 题型:
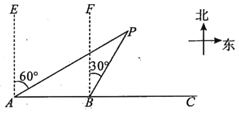
【题目】如图所示,![]() 城市在
城市在![]() 城市正东方向,现计划在
城市正东方向,现计划在![]() ,
,![]() 两城市间修建一条高速公路(即线段
两城市间修建一条高速公路(即线段![]() ).经测量,森林保护区的中心
).经测量,森林保护区的中心![]() 在城市
在城市![]() 的北偏东
的北偏东![]() 方向上,在线段
方向上,在线段![]() 上距
上距![]() 城市
城市![]() 的
的![]() 处测得
处测得![]() 在北偏东
在北偏东![]() 方向上,已知森林保护区是以点
方向上,已知森林保护区是以点![]() 为圆心,
为圆心,![]() 为半径的圆形区域.这条高速铁路是否会穿越保护区?请通过计算说明.(参考数据:
为半径的圆形区域.这条高速铁路是否会穿越保护区?请通过计算说明.(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
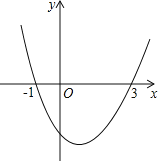
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于(-1,0),(3,0)两点,则下列说法:①abc<0;②a-b+c=0;③2a+b=0;④2a+c>0;⑤若A(x1,y1),B(x2,y2),C(x3,y3)为抛物线上三点,且-1<x1<x2<1,x3>3,则y2<y1<y3,其中正确的结论是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() x2+bx+c与x轴交于点A,B,与y轴交于点C,直线BC的解析式为y=﹣x+6.
x2+bx+c与x轴交于点A,B,与y轴交于点C,直线BC的解析式为y=﹣x+6.
(1)求抛物线的解析式;
(2)点M为线段BC上方抛物线上的任意一点,连接MB,MC,点N为抛物线对称轴上任意一点,当M到直线BC的距离最大时,求点M的坐标及MN+NB的最小值;
(3)在(2)中,点M到直线BC的距离最大时,连接OM交BC于点E,将原抛物线沿射线OM平移,平移后的抛物线记为y′,当y′经过点M时,它的对称轴与x轴的交点记为H.将△BOE绕点B逆时针旋转60°至△BO1E1,再将△BO1E1沿着直线O1H平移,得到△B1O2E2,在平面内是否存在点F,使以点C,H,B1,F为顶点的四边形是以B1H为边的菱形.若存在,直接写出点B1的横坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
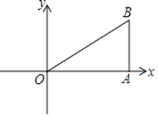
【题目】如图,在平面直角坐标系中,A(6,0),B(6,3),画出△ABO的所有以原点O为位似中心的△CDO,且△CDO与△ABO的相似比为1:3,并写出C、D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为直径作圆,交斜边AB于点E,D为AC的中点.连接DO,DE.则下列结论中不一定正确的是( )

A. DO∥ABB. △ADE是等腰三角形
C. DE⊥ACD. DE是⊙O的切线
查看答案和解析>>
科目:初中数学 来源: 题型:
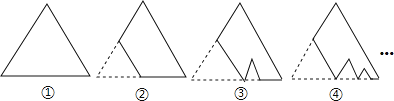
【题目】如图,图①是一块边长为1,周长记为P1的等边三角形纸板,沿图①的底边剪去一块边长的![]() 的等边三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的
的等边三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的![]() )后,得图③,④,…,记第n(n≥3)块纸板的周长为Pn,则Pn-Pn-1=_________
)后,得图③,④,…,记第n(n≥3)块纸板的周长为Pn,则Pn-Pn-1=_________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com