
【题目】如图,在平面直角坐标系中,A(6,0),B(6,3),画出△ABO的所有以原点O为位似中心的△CDO,且△CDO与△ABO的相似比为1:3,并写出C、D的坐标.
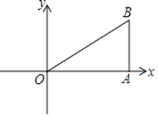
【答案】△CDO见详解;点C坐标为(2,0),点D坐标为(2,1)或C(-2,0),D(-2,-1).
【解析】
利用位似比分别得出符合题意的两种图形即可,利用相似三角形的性质求解可得C与D的坐标.
解;如图所示:两种情况,
∵A(6,0),B(6,3),
∴OA=6,AB=3,
∵△CDO与△ABO的相似比为1:3,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
解得:OC=2,CD=1,
∴C(2,0),D(2,1);
同理知C′(-2,0),D′(-2,-1).
综上,点C坐标为(2,0),点D坐标为(2,1)或C(-2,0),D(-2,-1).
故答案为:△CDO见详解;点C坐标为(2,0),点D坐标为(2,1)或C(-2,0),D(-2,-1).


科目:初中数学 来源: 题型:
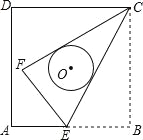
【题目】如图,正方形ABCD的边长为4,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°
(1)如图①,若∠ACD=60°,BC=1,CD=3,则AC的长为 ;
(2)如图②,若∠ACD=45°,BC=1,CD=3,求出AC的长;
(3)如图③,若∠ACD=30°,BC=a,CD=b,直接写出AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
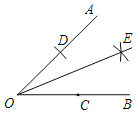
【题目】如图是小西设计的“作已知角∠AOB的平分线”的尺规作图过程:
①在射线OB上取一点C;
②以点O为圆心,OC长为半径作弧,交射线OA于点D;
③分别以点C,D为圆心,OC长为半径作弧,两弧相交于点E;
④作射线OE.
则射线OE即为∠AOB的角平分线.
请观察图形回答下列问题:
(1)由步骤②知,线段OC,OD的数量关系是______;连接DE,CE,线段CO,CE的数量关系是______;
(2)在(1)的条件下,若∠EOC=25°,求∠ECB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
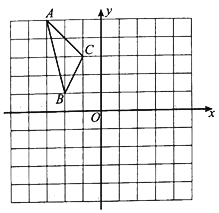
【题目】如图,在平面直角坐标系中,已知![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() ,
,![]() ,
,![]() .
.
(1)若![]() 经过平移后得到
经过平移后得到![]() ,已知点
,已知点![]() 的坐标为
的坐标为![]() ,写出顶点
,写出顶点![]() ,
,![]() 的坐标;
的坐标;
(2)若![]() 和
和![]() 关于原点
关于原点![]() 成中心对称图形,写出
成中心对称图形,写出![]() 各顶点的坐标;
各顶点的坐标;
(3)将![]() 绕着点O按顺时针方向旋转
绕着点O按顺时针方向旋转![]() 得到
得到![]() ,写出
,写出![]() 的各顶点的坐标.
的各顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
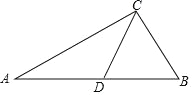
【题目】如图,在△ABC中,CD是边AB上的中线,∠B是锐角,sinB=![]() ,tanA=
,tanA=![]() ,AC=
,AC=![]() ,
,
(1)求∠B 的度数和 AB 的长.
(2)求 tan∠CDB 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应市政府关于“垃圾不落地![]() 市区更美丽”的主题宣传活动,郑州外国语中学随机调查了部分学生对垃圾分类知识的掌握情况,调查选项分为“A:非常了解;B:比较了解;C:了解较少;D:不了解
市区更美丽”的主题宣传活动,郑州外国语中学随机调查了部分学生对垃圾分类知识的掌握情况,调查选项分为“A:非常了解;B:比较了解;C:了解较少;D:不了解![]() ”四种,并将调查结果绘制成以下两幅不完整的统计图
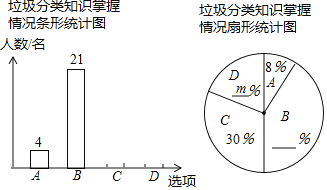
”四种,并将调查结果绘制成以下两幅不完整的统计图![]() 请根据图中提供的信息,解答下列问题;
请根据图中提供的信息,解答下列问题;
![]() 求
求![]() ______,并补全条形统计图;
______,并补全条形统计图;
![]() 若我校学生人数为1000名,根据调查结果,估计该校“非常了解”与“比较了解”的学生共有______名;
若我校学生人数为1000名,根据调查结果,估计该校“非常了解”与“比较了解”的学生共有______名;
![]() 已知“非常了解”的是3名男生和1名女生,从中随机抽取2名向全校做垃圾分类的知识交流,请画树状图或列表的方法,求恰好抽到1男1女的概率.
已知“非常了解”的是3名男生和1名女生,从中随机抽取2名向全校做垃圾分类的知识交流,请画树状图或列表的方法,求恰好抽到1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
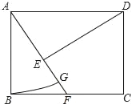
【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E
(1)求证:DE=AB;
(2)以A为圆心,AB长为半径作圆弧交AF于点G,若BF=FC=1,求扇形ABG的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“六一”儿童节那天,小强去商店买东西,看见每盒饼干的标价是整数,于是小强拿出10元钱递给商店的阿姨,下面是他俩的对话:小强:“阿姨,我有10元钱,想买一盒饼干和一袋牛奶.”阿姨:“小朋友,本来你用10元钱买一盒饼干是有钱多的,但要再买一袋牛奶钱就不够了.不过今天是儿童节,饼干打九折,两样东西请你拿好,找你8角钱.”如果每盒饼干和每袋牛奶的标价分别设为x元,y元,请你根据以上信息:
(1)请你求出x与y之间的关系式;(用含x的式子表示y)
(2)请你根据上述条件,求出每盒饼干和每袋牛奶的标价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com