
【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为直径作圆,交斜边AB于点E,D为AC的中点.连接DO,DE.则下列结论中不一定正确的是( )

A. DO∥ABB. △ADE是等腰三角形
C. DE⊥ACD. DE是⊙O的切线
【答案】C
【解析】
连接OE,由OD为三角形ABC的中位线,利用中位线定理得到OD与AB平行,选项A正确;由两直线平行得到同位角相等,内错角相等即∠COD=∠B,∠DOE=∠OEB,再由OE=OB,利用等边对等角得到∠OEB=∠B,等量代换得到∠COD=∠DOE,再由OC=OE,OD为公共边得到三角形COD与三角形EOD全等,由全等三角形的对应角相等得到∠OED=∠OCD为直角,即OE垂直于DE,可得出DE为圆O的切线,选项D正确;连接EC,由BC是直径可得∠AEC=∠CEB=90°,在直角三角形AEC中,D为斜边的中点,根据直角三角形斜边上的中线等于斜边的一半可得DE=AD,即三角形AED为等腰三角形,选项B正确,而DE不一定垂直于AC,故选项C符合题意.
连接OE
∵D为AC中点,O为BC中点
∴OD为△ABC的中位线,
∴DO∥AB,选项A正确;
∵∠COD=∠B,∠DOE=∠OEB,
∵OE=OB,
∴∠OEB=∠B,
∴∠COD=∠DOE,
在△COD和△EOD中,
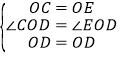 ,
,
∴△COD≌△EOD(SAS),
∴∠OED=∠OCD=90°,
∴DE为圆O的切线,选项D正确;
连接EC,∵BC是直径,
∴∠AEC=∠CEB=90°,
在RtAEC中,
∵AD=DC,
∴DE=AD,
∴△AED为等腰三角形,选项B正确,
则不一定正确的为DE⊥AC.
故选:C.



科目:初中数学 来源: 题型:
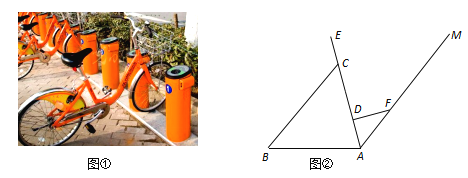
【题目】“低碳环保,你我同行”.近几年,各大城市的公共自行车给市民出行带来了极大的方便.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A.D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
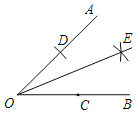
【题目】如图是小西设计的“作已知角∠AOB的平分线”的尺规作图过程:
①在射线OB上取一点C;
②以点O为圆心,OC长为半径作弧,交射线OA于点D;
③分别以点C,D为圆心,OC长为半径作弧,两弧相交于点E;
④作射线OE.
则射线OE即为∠AOB的角平分线.
请观察图形回答下列问题:
(1)由步骤②知,线段OC,OD的数量关系是______;连接DE,CE,线段CO,CE的数量关系是______;
(2)在(1)的条件下,若∠EOC=25°,求∠ECB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
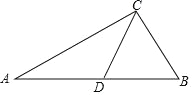
【题目】如图,在△ABC中,CD是边AB上的中线,∠B是锐角,sinB=![]() ,tanA=
,tanA=![]() ,AC=
,AC=![]() ,
,
(1)求∠B 的度数和 AB 的长.
(2)求 tan∠CDB 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
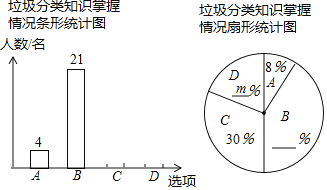
【题目】为响应市政府关于“垃圾不落地![]() 市区更美丽”的主题宣传活动,郑州外国语中学随机调查了部分学生对垃圾分类知识的掌握情况,调查选项分为“A:非常了解;B:比较了解;C:了解较少;D:不了解
市区更美丽”的主题宣传活动,郑州外国语中学随机调查了部分学生对垃圾分类知识的掌握情况,调查选项分为“A:非常了解;B:比较了解;C:了解较少;D:不了解![]() ”四种,并将调查结果绘制成以下两幅不完整的统计图
”四种,并将调查结果绘制成以下两幅不完整的统计图![]() 请根据图中提供的信息,解答下列问题;
请根据图中提供的信息,解答下列问题;
![]() 求
求![]() ______,并补全条形统计图;
______,并补全条形统计图;
![]() 若我校学生人数为1000名,根据调查结果,估计该校“非常了解”与“比较了解”的学生共有______名;
若我校学生人数为1000名,根据调查结果,估计该校“非常了解”与“比较了解”的学生共有______名;
![]() 已知“非常了解”的是3名男生和1名女生,从中随机抽取2名向全校做垃圾分类的知识交流,请画树状图或列表的方法,求恰好抽到1男1女的概率.
已知“非常了解”的是3名男生和1名女生,从中随机抽取2名向全校做垃圾分类的知识交流,请画树状图或列表的方法,求恰好抽到1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的四个顶点分别在反比例函数![]() 与
与![]() (x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(1)当m=4,n=20时.
①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
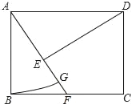
【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E
(1)求证:DE=AB;
(2)以A为圆心,AB长为半径作圆弧交AF于点G,若BF=FC=1,求扇形ABG的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
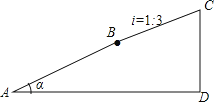
【题目】小林从点A出发,沿着坡角为α的斜坡向上走了650米到达点B,且sinα=![]() .然后又沿着坡度i=1:3的斜坡向上走了500米达到点C.
.然后又沿着坡度i=1:3的斜坡向上走了500米达到点C.
(1)小明从A点到B点上升的高度是多少米?
(2)小明从A点到C点上升的高度CD是多少米?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
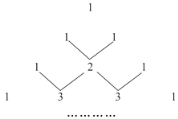
【题目】我国古代数学家的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图这个三角形的构造法其两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.利用 规律计算:25-5×24+10×23-10×22+5×2-1的值为____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com