
【题目】若平面直角坐标系内的点M满足横、纵坐标都为整数,则把点M叫做“整点”.例如:P(1,0)、Q(2,﹣2)都是“整点”.抛物线y=mx2﹣4mx+4m-2(m![]() 0)与x轴交于点A、B两点,若该抛物线在A、B之间的部分与线段AB所围成的区域(包括边界)恰有七个整点,则m的取值范围是( )
0)与x轴交于点A、B两点,若该抛物线在A、B之间的部分与线段AB所围成的区域(包括边界)恰有七个整点,则m的取值范围是( )
A. ![]() <m≤1B.
<m≤1B. ![]() ≤m<1C. 1<m≤2D. 1<m<2
≤m<1C. 1<m≤2D. 1<m<2
【答案】A
【解析】
画出图象,利用图象可得m的取值范围
∵y=mx2-4mx+4m-2=m(x-2)2-2且m>0,
∴该抛物线开口向上,顶点坐标为(2,-2),对称轴是直线x=2.
由此可知点(2,0)、点(2,-1)、顶点(2,-2)符合题意.
①当该抛物线经过点(1,-1)和(3,-1)时(如答案图1),这两个点符合题意.
将(1,-1)代入y=mx2-4mx+4m-2得到-1=m-4m+4m-2.解得m=1.
此时抛物线解析式为y=x2-4x+2.
由y=0得x2-4x+2=0.解得x1=2-![]() ≈0.6,x2=2+
≈0.6,x2=2+![]() ≈3.4.
≈3.4.
∴x轴上的点(1,0)、(2,0)、(3,0)符合题意.
则当m=1时,恰好有(1,0)、(2,0)、(3,0)、(1,-1)、(3,-1)、(2,-1)、(2,-2)这7个整点符合题意.
∴m≤1.【注:m的值越大,抛物线的开口越小,m的值越小,抛物线的开口越大】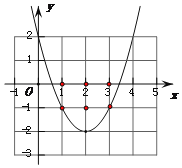
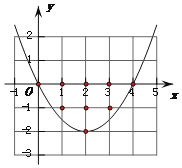
答案图1(m=1时)答案图2(m=![]() 时)
时)
②当该抛物线经过点(0,0)和点(4,0)时(如答案图2),这两个点符合题意.
此时x轴上的点(1,0)、(2,0)、(3,0)也符合题意.
将(0,0)代入y=mx2-4mx+4m-2得到0=0-4m+0-2.解得m=![]() ,
,
此时抛物线解析式为y=![]() x2-2x.
x2-2x.
当x=1时,得y=![]() ×1-2×1=-
×1-2×1=-![]() <-1.∴点(1,-1)符合题意.
<-1.∴点(1,-1)符合题意.
当x=3时,得y=![]() ×9-2×3=-
×9-2×3=-![]() <-1.∴点(3,-1)符合题意.
<-1.∴点(3,-1)符合题意.
综上可知:当m=![]() 时,点(0,0)、(1,0)、(2,0)、(3,0)、(4,0)、(1,-1)、(3,-1)、(2,-2)、(2,-1)都符合题意,共有9个整点符合题意,
时,点(0,0)、(1,0)、(2,0)、(3,0)、(4,0)、(1,-1)、(3,-1)、(2,-2)、(2,-1)都符合题意,共有9个整点符合题意,
∴m=![]() 不符合题.
不符合题.
∴m>![]() .
.
综合①②可得:当![]() <m≤1时,该函数的图象与x轴所围成的区域(含边界)内有七个整点,
<m≤1时,该函数的图象与x轴所围成的区域(含边界)内有七个整点,
故选:A.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,⊙O过正方形ABCD的顶点A、D且与边BC相切于点E,分别交AB、DC于点M、N.动点P在⊙O或正方形ABCD的边上以每秒一个单位的速度做连续匀速运动.设运动的时间为x,圆心O与P点的距离为y,图2记录了一段时间里y与x的函数关系,在这段时间里P点的运动路径为( )

A. 从D点出发,沿弧DA→弧AM→线段BM→线段BC
B. 从B点出发,沿线段BC→线段CN→弧ND→弧DA
C. 从A点出发,沿弧AM→线段BM→线段BC→线段CN
D. 从C点出发,沿线段CN→弧ND→弧DA→线段AB
查看答案和解析>>
科目:初中数学 来源: 题型:
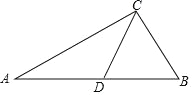
【题目】如图,在△ABC中,CD是边AB上的中线,∠B是锐角,sinB=![]() ,tanA=
,tanA=![]() ,AC=
,AC=![]() ,
,
(1)求∠B 的度数和 AB 的长.
(2)求 tan∠CDB 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的四个顶点分别在反比例函数![]() 与
与![]() (x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(1)当m=4,n=20时.
①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
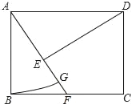
【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E
(1)求证:DE=AB;
(2)以A为圆心,AB长为半径作圆弧交AF于点G,若BF=FC=1,求扇形ABG的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,直线L:y=mx+n(m<0,n>0)与x,y轴分别相交于A,B两点,将△AOB绕点O逆时针旋转90°,得到△COD,过点A,B,D的抛物线P叫做L的关联抛物线,而L叫做P的关联直线.
(1)若L:y=-x+2,则P表示的函数解析式为______;若P:![]() ,则
,则![]() 表示的函数解析式为_______.
表示的函数解析式为_______.
(2)如图②,若L:y=-3x+3,P的对称轴与CD相交于点E,点F在L上,点Q在P的对称轴上.当以点C,E,Q,F为顶点的四边形是以CE为一边的平行四边形时,求点Q的坐标;
(3)如图③,若L:y=mx+1,G为AB中点,H为CD中点,连接GH,M为GH中点,连接OM.若OM=![]() ,求出L,P表示的函数解析式.
,求出L,P表示的函数解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
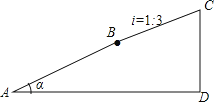
【题目】小林从点A出发,沿着坡角为α的斜坡向上走了650米到达点B,且sinα=![]() .然后又沿着坡度i=1:3的斜坡向上走了500米达到点C.
.然后又沿着坡度i=1:3的斜坡向上走了500米达到点C.
(1)小明从A点到B点上升的高度是多少米?
(2)小明从A点到C点上升的高度CD是多少米?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在直角梯形ABCD中,AD∥BC,DC⊥BC,P是边AB上一动点,PE⊥CD,垂足为点E,PM⊥AB,交边CD于点M,AD=1,AB=5,CD=4.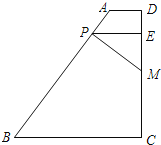
(1)求证:∠PME=∠B;
(2)设A、P两点的距离为x,EM=y,求y关于x的函数解析式,并写出它的定义域;
(3)连接PD,当△PDM是以PM为腰的等腰三角形时,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
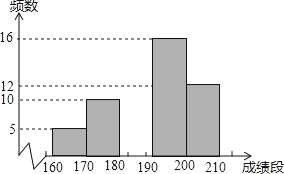
【题目】我校为了迎接体育中考,了解学生的体育成绩,从全校1000名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制作图如下:
成绩段 | 频数 | 频率 |
160≤x<170 | 5 | 0.1 |
170≤x<180 | 10 | a |
180≤x<190 | b | 0.14 |
190≤x<200 | 16 | c |
200≤x<210 | 12 | 0.24 |
根据图表解决下列问题:
(1)本次共抽取了 名学生进行体育测试,表中,a= ,b= ,c= ;
(2)补全统计图;
(3)“跳绳”数在180(包括180)以上,则此项成绩可得满分.那么,你估计全校九年级有多少学生在此项成绩中获满分?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com