
ΓΨΧβΡΩΓΩΈ“–ΘΈΣΝΥ”≠Ϋ”Χε”ΐ÷–ΩΦΘ§ΝΥΫβ―ß…ζΒΡΧε”ΐ≥…Φ®Θ§¥”»Ϊ–Θ1000ΟϊΨ≈ΡξΦΕ―ß…ζ÷–ΥφΜζ≥ι»ΓΝΥ≤ΩΖ÷―ß…ζΫχ––Χε”ΐ≤β ‘Θ§Τδ÷–ΓΑΧχ…ΰΓ±≥…Φ®÷ΤΉςΆΦ»γœ¬ΘΚ
≥…Φ®ΕΈ | ΤΒ ΐ | ΤΒ¬ |
160ΓήxΘΦ170 | 5 | 0.1 |
170ΓήxΘΦ180 | 10 | a |
180ΓήxΘΦ190 | b | 0.14 |
190ΓήxΘΦ200 | 16 | c |
200ΓήxΘΦ210 | 12 | 0.24 |
ΗυΨίΆΦ±μΫβΨωœ¬Ν–Έ ΧβΘΚ
(1)±Ψ¥ΈΙ≤≥ι»ΓΝΥΓΓ Οϊ―ß…ζΫχ––Χε”ΐ≤β ‘Θ§±μ÷–Θ§aΘΫΓΓΓΓΘ§bΘΫΓΓΘ§cΘΫΓΓΓΓΘΜ
(2)≤Ι»ΪΆ≥ΦΤΆΦΘΜ
(3)ΓΑΧχ…ΰΓ± ΐ‘Ύ180(Αϋά®180)“‘…œΘ§‘ρ¥Υœν≥…Φ®Ω…ΒΟ¬ζΖ÷Θ°Ρ«Ο¥Θ§ΡψΙάΦΤ»Ϊ–ΘΨ≈ΡξΦΕ”–Εύ…Ό―ß…ζ‘Ύ¥Υœν≥…Φ®÷–Μώ¬ζΖ÷ΘΩ
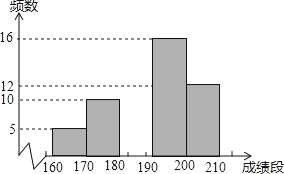
ΓΨ¥πΑΗΓΩ(1)50ΘΜ0.2ΘΜ7ΘΜ0.32ΘΜ(2)≤ΙΆΦΦϊΫβΈωΘΜ(3)ΙάΦΤ»Ϊ–ΘΨ≈ΡξΦΕ”–700Οϊ―ß…ζ‘Ύ¥Υœν≥…Φ®÷–Μώ¬ζΖ÷Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨί≥…Φ®ΕΈ160ΓήxΘΦ170ΒΡΤΒ ΐ”κΤΒ¬ «σ≥ω≥ι»Γ―ß…ζΉή ΐΘ§ΫχΕχ«σ≥ωaΘ§bΘ§cΒΡ÷ΒΦ¥Ω…ΘΜ
Θ®2Θ©ΗυΨί≥…Φ®ΕΈ180ΓήxΘΦ190ΒΡΤΒ ΐΘ§≤Ι»ΪΆ≥ΦΤΆΦΦ¥Ω…ΘΜ
Θ®3Θ©ΗυΨίΓΑΧχ…ΰΓ± ΐ‘Ύ180Θ®Αϋά®180Θ©“‘…œ»Υ ΐΒΡΤΒ¬ ≥Υ“‘1000Φ¥Ω…ΒΟΒΫΫαΙϊΘ°
(1)ΗυΨίΧβ“βΒΟΘΚ5Γ¬0.1ΘΫ50ΘΜaΘΫ10Γ¬50ΘΫ0.2ΘΜbΘΫ50ΓΝ0.14ΘΫ7ΘΜcΘΫ16Γ¬50ΘΫ0.32Θ§
Ι ¥πΑΗΈΣΘΚ50ΘΜ0.2ΘΜ7ΘΜ0.32ΘΜ
(2)≥…Φ®ΕΈ180ΓήxΘΦ190ΒΡΤΒ ΐΈΣ7Θ§≤Ι»ΪΆ≥ΦΤΆΦΘ§»γΆΦΥυ ΨΘΚ
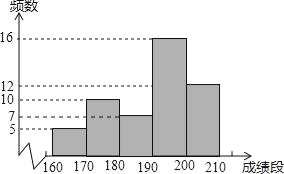 ΘΜ
ΘΜ
(3)ΗυΨίΧβ“βΒΟΘΚ1000ΓΝ(0.14+0.32+0.24)ΘΫ700(Οϊ)Θ§
‘ρΙάΦΤ»Ϊ–ΘΨ≈ΡξΦΕ”–700Οϊ―ß…ζ‘Ύ¥Υœν≥…Φ®÷–Μώ¬ζΖ÷Θ°


 ΒΦ―ß»Ϊ≥ΧΝΖ¥¥”≈―ΒΝΖœΒΝ–¥πΑΗ
ΒΦ―ß»Ϊ≥ΧΝΖ¥¥”≈―ΒΝΖœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»τΤΫΟφ÷±Ϋ«Ήχ±ξœΒΡΎΒΡΒψM¬ζΉψΚαΓΔΉίΉχ±ξΕΦΈΣ’ϊ ΐΘ§‘ρΑ―ΒψMΫ–ΉωΓΑ’ϊΒψΓ±Θ°άΐ»γΘΚP(1Θ§0)ΓΔQ(2Θ§©¹2)ΕΦ «ΓΑ’ϊΒψΓ±Θ°≈ΉΈοœΏyΘΫmx2©¹4mx+4m-2(m![]() 0)”κx÷αΫΜ”ΎΒψAΓΔBΝΫΒψΘ§»τΗΟ≈ΉΈοœΏ‘ΎAΓΔB÷°ΦδΒΡ≤ΩΖ÷”κœΏΕΈABΥυΈß≥…ΒΡ«χ”ρ(Αϋά®±ΏΫγ)«Γ”–ΤΏΗω’ϊΒψΘ§‘ρmΒΡ»Γ÷ΒΖΕΈß «( )
0)”κx÷αΫΜ”ΎΒψAΓΔBΝΫΒψΘ§»τΗΟ≈ΉΈοœΏ‘ΎAΓΔB÷°ΦδΒΡ≤ΩΖ÷”κœΏΕΈABΥυΈß≥…ΒΡ«χ”ρ(Αϋά®±ΏΫγ)«Γ”–ΤΏΗω’ϊΒψΘ§‘ρmΒΡ»Γ÷ΒΖΕΈß «( )
A. ![]() <mΓή1B.
<mΓή1B. ![]() Γήm<1C. 1<mΓή2D. 1<m<2
Γήm<1C. 1<mΓή2D. 1<m<2
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
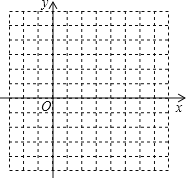
ΓΨΧβΡΩΓΩ“―÷Σ≈ΉΈοœΏ![]()
![]() Ε‘≥Τ÷αΈΣ______Θ§ΕΞΒψΉχ±ξΈΣ______ΘΜ
Ε‘≥Τ÷αΈΣ______Θ§ΕΞΒψΉχ±ξΈΣ______ΘΜ
![]() ‘ΎΉχ±ξœΒ÷–άϊ”ΟΈεΒψΖ®Μ≠≥ω¥Υ≈ΉΈοœΏΘ°
‘ΎΉχ±ξœΒ÷–άϊ”ΟΈεΒψΖ®Μ≠≥ω¥Υ≈ΉΈοœΏΘ°
x |
| ______ | ______ | ______ | ______ | ______ |
|
y |
| ______ | ______ | ______ | ______ | ______ |
|
![]() »τ≈ΉΈοœΏ”κx÷αΫΜΒψΈΣAΓΔBΘ§Βψ
»τ≈ΉΈοœΏ”κx÷αΫΜΒψΈΣAΓΔBΘ§Βψ![]() ‘Ύ≈ΉΈοœΏ…œΘ§«σ
‘Ύ≈ΉΈοœΏ…œΘ§«σ![]() ΒΡΟφΜΐΘ°
ΒΡΟφΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
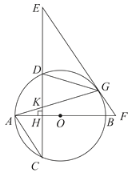
ΓΨΧβΡΩΓΩ»γΆΦΘ§AB «Γ―OΒΡ÷±ΨΕΘ§œ“CDΓΆAB”ΎHΘ§GΈΣΓ―O…œ“ΜΒψΘ§Ν§Ϋ”AGΫΜCD”ΎKΘ§‘ΎCDΒΡ―”≥ΛœΏ…œ»Γ“ΜΒψEΘ§ ΙEG=EKΘ§EGΒΡ―”≥ΛœΏΫΜABΒΡ―”≥ΛœΏ”ΎFΘ°
Θ®1Θ©«σ÷ΛΘΚEF «Γ―OΒΡ«–œΏΘΜ
Θ®2Θ©Ν§Ϋ”DGΘ§»τACΓΈEF ±Θ°
ΔΌ«σ÷ΛΘΚΓςKGDΓΉΓςKEGΘΜ
ΔΎ»τ![]() Θ§AK=
Θ§AK=![]() Θ§«σBFΒΡ≥ΛΘ°
Θ§«σBFΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΫΪΓςOAB»ΤOΒψΡφ ±’κ–ΐΉΣ60ΓψΒΟΒΫΓςOCDΘ§»τOAΘΫ4Θ§ΓœAOBΘΫ35ΓψΘ§‘ρœ¬Ν–Ϋα¬έ¥μΈσΒΡ «Θ®ΓΓΓΓΘ©
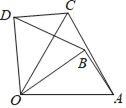
A. ΓœBDOΘΫ60Γψ B. ΓœBOCΘΫ25Γψ C. OCΘΫ4 D. BDΘΫ4
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ÷±œΏlΨ≠ΙΐA(6Θ§0)ΚΆB(0Θ§12)ΝΫΒψΘ§«“”κ÷±œΏyΘΫxΫΜ”ΎΒψCΘ§ΒψP(mΘ§0)‘Ύx÷α…œ‘ΥΕ·Θ°
(1)«σ÷±œΏlΒΡΫβΈω ΫΘΜ
(2)ΙΐΒψPΉςlΒΡΤΫ––œΏΫΜ÷±œΏyΘΫx”ΎΒψDΘ§Β±mΘΫ3 ±Θ§«σΓςPCDΒΡΟφΜΐΘΜ
(3) «Ζώ¥φ‘ΎΒψPΘ§ ΙΒΟΓςPCA≥…ΈΣΒ»―ϋ»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ωΥυ”–ΖϊΚœΧθΦΰΒΡΒψPΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘ§»γΆΦΘ§÷±œΏMNΫΜΓ―O”ΎAΘ§BΝΫΒψΘ§AC «÷±ΨΕΘ§ADΤΫΖ÷ΓœCAMΫΜΓ―O”ΎDΘ§ΙΐDΉςDEΓΆMN”ΎEΘ°
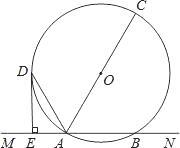
Θ®1Θ©«σ÷ΛΘΚDE «Γ―OΒΡ«–œΏΘΜ
Θ®2Θ©»τDE=6cmΘ§AE=3cmΘ§«σΓ―OΒΡΑκΨΕΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ![]() ABCD÷–Θ§EΓΔFΖ÷±π «ADΓΔBC…œΒΡΒψΘ§ΫΪΤΫ––ΥΡ±Ώ–ΈABCD―ΊEFΥυ‘Ύ÷±œΏΖ≠’έΘ§ ΙΒψB”κΒψD÷ΊΚœΘ§«“ΒψA¬δ‘ΎΒψAΓδ¥ΠΘ°
ABCD÷–Θ§EΓΔFΖ÷±π «ADΓΔBC…œΒΡΒψΘ§ΫΪΤΫ––ΥΡ±Ώ–ΈABCD―ΊEFΥυ‘Ύ÷±œΏΖ≠’έΘ§ ΙΒψB”κΒψD÷ΊΚœΘ§«“ΒψA¬δ‘ΎΒψAΓδ¥ΠΘ°
Θ®1Θ©«σ÷ΛΘΚΓςAΓδEDΓ’ΓςCFDΘΜ
Θ®2Θ©Ν§ΫαBEΘ§»τΓœEBF=60ΓψΘ§EF=3Θ§«σΥΡ±Ώ–ΈBFDEΒΡΟφΜΐΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
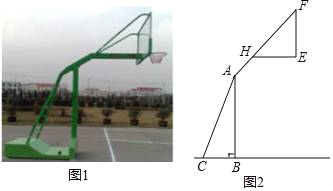
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§2Ζ÷±π «Ρ≥ΩνάΚ«ρΦήΒΡ ΒΈοΆΦ”κ Ψ“βΆΦΘ§“―÷ΣABΓΆBC”ΎΒψBΘ§ΒΉΉυBCΒΡ≥ΛΈΣ1ΟΉΘ§ΒΉΉυBC”κ÷ßΦήACΥυ≥…ΒΡΫ«ΓœACBΘΫ60ΓψΘ§ΒψH‘Ύ÷ßΦήAF…œΘ§άΚΑεΒΉ≤Ω÷ßΦήEHΓΈBCΘ§EFΓΆEH”ΎΒψEΘ§“―÷ΣAH≥Λ![]() ΟΉΘ§HF≥Λ
ΟΉΘ§HF≥Λ![]() ΟΉΘ§HE≥Λ1ΟΉΘ°
ΟΉΘ§HE≥Λ1ΟΉΘ°
(1)«σάΚΑεΒΉ≤Ω÷ßΦήHE”κ÷ßΦήAFΥυ≥…ΒΡΫ«ΓœFHEΒΡΕ» ΐΘ°
(2)«σάΚΑεΒΉ≤ΩΒψEΒΫΒΊΟφΒΡΨύάκΘ°(ΫαΙϊ±ΘΝτΗυΚ≈)
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com