
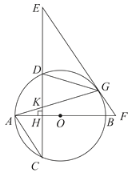
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,G为⊙O上一点,连接AG交CD于K,在CD的延长线上取一点E,使EG=EK,EG的延长线交AB的延长线于F.
(1)求证:EF是⊙O的切线;
(2)连接DG,若AC∥EF时.
①求证:△KGD∽△KEG;
②若![]() ,AK=
,AK=![]() ,求BF的长.
,求BF的长.
【答案】(1)见解析;(2)①见解析,②![]()
【解析】
(1)连接OG.根据切线的判定,证出∠KGE+∠OGA=90°,故EF是⊙O的切线.(2)①证∠E=∠AGD,又∠DKG=∠CKE,故△KGD∽△KGE.②连接OG.![]() ,设
,设![]() ,
,![]() ,
,![]() ,则
,则![]() ,在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,即
,在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,即![]() ;由勾股定理得:OH2+CH2=OC2,
;由勾股定理得:OH2+CH2=OC2,![]() ;在Rt△OGF中,
;在Rt△OGF中,![]() ,
,![]() ,
,![]()
(1)如图,连接OG.∵EG=EK,
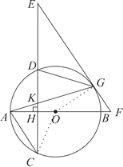
∴∠KGE=∠GKE=∠AKH,
又OA=OG,∴∠OGA=∠OAG,
∵CD⊥AB,∴∠AKH+∠OAG=90°,
∴∠KGE+∠OGA=90°,
∴EF是⊙O的切线.
(2)①∵AC∥EF,∴∠E=∠C,
又∠C=∠AGD,∴∠E=∠AGD,
又∠DKG=∠CKE,
∴△KGD∽△KGE.
②连接OG,如图所示.∵![]() ,AK=
,AK=![]() ,
,
设![]() ,∴
,∴![]() ,
,![]() ,则
,则![]()
KE=GE,AC∥EF,∴CK=AC=5k,∴HK=CK-CH=k.
在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,
即![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
设⊙O半径为R,在Rt△OCH中,OC=R,OH=R-3k,CH=4k,
由勾股定理得:OH2+CH2=OC2,![]() ,∴
,∴![]()
在Rt△OGF中,![]() ,∴
,∴![]() ,
,
∴![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的四个顶点分别在反比例函数![]() 与
与![]() (x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(1)当m=4,n=20时.
①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在直角梯形ABCD中,AD∥BC,DC⊥BC,P是边AB上一动点,PE⊥CD,垂足为点E,PM⊥AB,交边CD于点M,AD=1,AB=5,CD=4.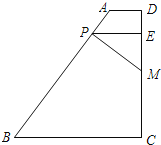
(1)求证:∠PME=∠B;
(2)设A、P两点的距离为x,EM=y,求y关于x的函数解析式,并写出它的定义域;
(3)连接PD,当△PDM是以PM为腰的等腰三角形时,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
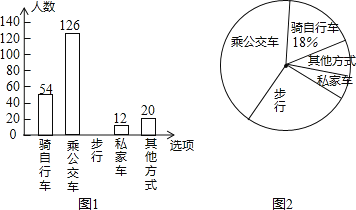
【题目】为了解全校学生上学的交通方式,该校九年级![]() 班的4名同学联合设计了一份调查问卷,对该校部分学生进行了随机调查
班的4名同学联合设计了一份调查问卷,对该校部分学生进行了随机调查![]() 按
按![]() 骑自行车
骑自行车![]() 、
、![]() 乘公交车
乘公交车![]() 、
、![]() 步行
步行![]() 、
、![]() 乘私家车
乘私家车![]() 、
、![]() 其他方式
其他方式![]() 设置选项,要求被调查同学从中单选,并将调查结果绘制成条形统计图1和扇形统计图2,根据以上信息,解答下列问题:
设置选项,要求被调查同学从中单选,并将调查结果绘制成条形统计图1和扇形统计图2,根据以上信息,解答下列问题:
![]() 本次接受调查的总人数是______人,并把条形统计图补充完整;
本次接受调查的总人数是______人,并把条形统计图补充完整;
![]() 在扇形统计图中,“乘私家车的人数所占的百分比是______,“其他方式”所在扇形的圆心角度数是______度;
在扇形统计图中,“乘私家车的人数所占的百分比是______,“其他方式”所在扇形的圆心角度数是______度;
![]() 已知这4名同学中有2名女同学,要从中选两名同学汇报调查结果,请你用列表法或画树状图的方法,求出恰好选出1名男生和1名女生的概率.
已知这4名同学中有2名女同学,要从中选两名同学汇报调查结果,请你用列表法或画树状图的方法,求出恰好选出1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学家的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图这个三角形的构造法其两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.利用 规律计算:25-5×24+10×23-10×22+5×2-1的值为____.
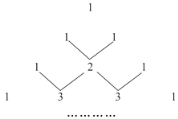
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为2cm,∠DAB=60°.点P从A点出发,以![]() cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动,设点P运动的时间为t(s).
cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动,设点P运动的时间为t(s).
(1)对角线AC的长是 cm;
(2)当P异于A、C时,请说明PQ∥BC;
(3)以P为圆心、PQ长为半径作圆,请问:在整个运动过程中,t为怎样的值时,⊙P与边BC分别有1个公共点和2个公共点?
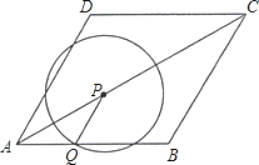
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校为了迎接体育中考,了解学生的体育成绩,从全校1000名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制作图如下:
成绩段 | 频数 | 频率 |
160≤x<170 | 5 | 0.1 |
170≤x<180 | 10 | a |
180≤x<190 | b | 0.14 |
190≤x<200 | 16 | c |
200≤x<210 | 12 | 0.24 |
根据图表解决下列问题:
(1)本次共抽取了 名学生进行体育测试,表中,a= ,b= ,c= ;
(2)补全统计图;
(3)“跳绳”数在180(包括180)以上,则此项成绩可得满分.那么,你估计全校九年级有多少学生在此项成绩中获满分?
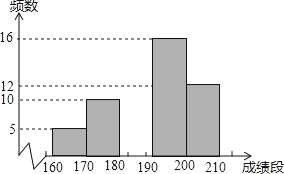
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,直径CD垂直于不过圆心O的弦AB,垂足为点N,连接AC,BC,点E在AB上,且AE=CE.
(1)求证:∠ABC=∠ACE;
(2)过点B作⊙O的切线交EC的延长线于点P,证明PB=PE;
(3)在第(2)问的基础上,设⊙O半径为2![]() ,若点N为OC中点,点Q在⊙O上,求线段PQ的最大值.
,若点N为OC中点,点Q在⊙O上,求线段PQ的最大值.
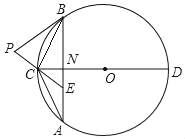
查看答案和解析>>
科目:初中数学 来源: 题型:
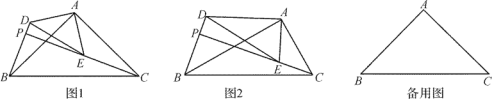
【题目】△ABC和△ADE是有公共顶点的三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.
(1) ①如图1,∠ADE=∠ABC=45°,求证:∠ABD=∠ACE.
②如图2,∠ADE=∠ABC=30°,①中的结论是否成立?请说明理由.
(2)在(1) ①的条件下,AB=6,AD=4,若把△ADE绕点A旋转,当∠EAC=90°时,画图并求PB的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com