
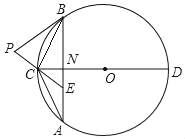
【题目】如图,在⊙O中,直径CD垂直于不过圆心O的弦AB,垂足为点N,连接AC,BC,点E在AB上,且AE=CE.
(1)求证:∠ABC=∠ACE;
(2)过点B作⊙O的切线交EC的延长线于点P,证明PB=PE;
(3)在第(2)问的基础上,设⊙O半径为2![]() ,若点N为OC中点,点Q在⊙O上,求线段PQ的最大值.
,若点N为OC中点,点Q在⊙O上,求线段PQ的最大值.
【答案】(1)详见解析;(2)详见解析;(3)![]()
【解析】
(1)因为直径CD垂直于不过圆心O的弦AB,垂足为点N,所以![]() ,所以∠CAE=∠ABC,因为AE=CE,所以∠CAE=∠ACE,所以∠ABC=∠ACE;
,所以∠CAE=∠ABC,因为AE=CE,所以∠CAE=∠ACE,所以∠ABC=∠ACE;
(2)连接OB,设∠CAE=∠ACE=∠ABC=x,通过计算可得∠PEB=∠PBE=2x,所以PB=PE;
(3)连接OP,证明△OBC和△PBE为等边三角形,因为⊙O半径为2![]() ,可得BN=3,NE=1,即PB=BE=4,在Rt△PBO中求得PO的长,即可得出PQ的最大值.
,可得BN=3,NE=1,即PB=BE=4,在Rt△PBO中求得PO的长,即可得出PQ的最大值.
解:(1)证明:∵直径CD垂直于不过圆心O的弦AB,垂足为点N,
∴![]() ,
,
∴∠CAE=∠ABC,
∵AE=CE,
∴∠CAE=∠ACE,
∴∠ABC=∠ACE;
(2)如图,连接OB,
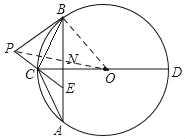
∵过点B作⊙O的切线交EC的延长线于点P,
∴∠OBP=90°,
设∠CAE=∠ACE=∠ABC=x,
则∠PEB=2x,
∵OB=OC,AB⊥CD,
∴∠OBC=∠OCB=90°﹣x,
∴∠BOC=180°﹣2(90°﹣x)=2x,
∴∠OBE=90°﹣2x,
∴∠PBE=90°﹣(90°﹣2x)=2x,
∴∠PEB=∠PBE,
∴PB=PE;
(3)如图,连接OP,
∵点N为OC中点,AB⊥CD,
∴AB是CD的垂直平分线,
∴BC=OB=OC,
∴△OBC为等边三角形,
∵⊙O半径为![]() ,
,
∴CN=![]() ,
,
∵∠CAE=∠ACE=![]() ∠BOC=30°,
∠BOC=30°,
∴∠CEN=60°,∠PBE=2∠CAB=60°,
∴△PBE为等边三角形,BN=3,NE=1,
∴PB=BE=BN+NE=3+1=4,
∴PO=![]() =
=![]() ,
,
∴PQ的最大值为PO+![]() =
=![]() +
+![]() .
.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知点![]() 的坐标为
的坐标为![]() .
.
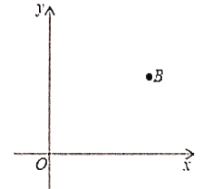
(1)请用直尺(不带刻度)和圆规作一条直线![]() ,它与
,它与![]() 轴和
轴和![]() 轴的正半轴分别交于点
轴的正半轴分别交于点![]() 和点
和点![]() ,且
,且![]() 与
与![]() 关于直线
关于直线![]() 对称.(作图不必写作法,但要保留作图痕迹.)
对称.(作图不必写作法,但要保留作图痕迹.)
(2)请求出(1)中作出的直线![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
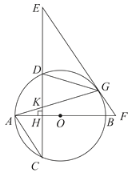
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,G为⊙O上一点,连接AG交CD于K,在CD的延长线上取一点E,使EG=EK,EG的延长线交AB的延长线于F.
(1)求证:EF是⊙O的切线;
(2)连接DG,若AC∥EF时.
①求证:△KGD∽△KEG;
②若![]() ,AK=
,AK=![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l经过A(6,0)和B(0,12)两点,且与直线y=x交于点C,点P(m,0)在x轴上运动.
(1)求直线l的解析式;
(2)过点P作l的平行线交直线y=x于点D,当m=3时,求△PCD的面积;
(3)是否存在点P,使得△PCA成为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
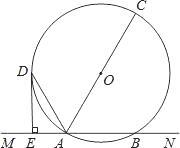
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c与x轴交于A,B两点,顶点C的纵坐标为﹣2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论:①b>0;②a﹣b+c<0;③阴影部分的面积为4;④若c=﹣1,则b2=4a.其中正确的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() ABCD中,E、F分别是AD、BC上的点,将平行四边形ABCD沿EF所在直线翻折,使点B与点D重合,且点A落在点A′处.
ABCD中,E、F分别是AD、BC上的点,将平行四边形ABCD沿EF所在直线翻折,使点B与点D重合,且点A落在点A′处.
(1)求证:△A′ED≌△CFD;
(2)连结BE,若∠EBF=60°,EF=3,求四边形BFDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,sinA=![]() ,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
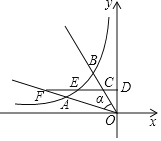
【题目】如图,角α的两边与双曲线y=![]() (k<0,x<0)交于A、B两点,在OB上取点C,作CD⊥y轴于点D,分别交双曲线y=
(k<0,x<0)交于A、B两点,在OB上取点C,作CD⊥y轴于点D,分别交双曲线y=![]() 、射线OA于点E、F,若OA=2AF,OC=2CB,则
、射线OA于点E、F,若OA=2AF,OC=2CB,则![]() 的值为______.
的值为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com