
����Ŀ����ͼ�٣�ֱ��L��y=mx+n(m<0��n>0)��x��y��ֱ��ཻ��A��B���㣬����AOB�Ƶ�O��ʱ����ת90�����õ���COD������A��B��D��������P����L�Ĺ��������ߣ���L����P�Ĺ���ֱ�ߣ�
(1)��L��y=-x+2����P��ʾ�ĺ�������ʽΪ______����P��![]() ����
����![]() ��ʾ�ĺ�������ʽΪ_______��
��ʾ�ĺ�������ʽΪ_______��
(2)��ͼ�ڣ���L��y=-3x+3��P�ĶԳ�����CD�ཻ�ڵ�E����F��L�ϣ���Q��P�ĶԳ����ϣ����Ե�C��E��Q��FΪ������ı�������CEΪһ�ߵ�ƽ���ı���ʱ�����Q�����ꣻ
(3)��ͼ�ۣ���L��y=mx+1��GΪAB�е㣬HΪCD�е㣬����GH��MΪGH�е㣬����OM����OM=![]() �����L��P��ʾ�ĺ�������ʽ��
�����L��P��ʾ�ĺ�������ʽ��

���𰸡�(1)![]() ��y=��2x+4��(2)Q����ΪQ1(��1��
��y=��2x+4��(2)Q����ΪQ1(��1��![]() )��Q2(��1��
)��Q2(��1��![]() )��(3)y=��3x+1��y=��3x2��2x+1��
)��(3)y=��3x+1��y=��3x2��2x+1��
��������
��1����l��y=-x+2�������A��B��D�����꣬���ô���ϵ�������P��ʾ�ĺ�������ʽ����P��![]() �������D��A��B�����꣬�����ô���ϵ�������l��ʾ�ĺ�������ʽ��
�������D��A��B�����꣬�����ô���ϵ�������l��ʾ�ĺ�������ʽ��
��2�����ݶԳ���Ķ����ɣ�
��3���Ե�C��E��Q��FΪ������ı�������CEΪһ�ߵ�ƽ���ı���ʱ������FQ��CE����FQ=CE���Դ�Ϊ�������з��������Q�����꣮ע�⣺��Q�����������������ͼ��ʾ����Ҫ©�⣻
��4�����ͼ��ʾ���������ߣ��������ֱ��������OGH�����OG�ij��ȣ�������AB=2OG���AB�ij��ȣ������ù��ɶ������y=mx+1��m��ֵ�����ֱ����l��P��ʾ�ĺ�������ʽ��
�⣺(1)![]() ��y=��2x+4��
��y=��2x+4��
(2)��![]() ��y=��3x+3����A(1��0)��B(0��3)��
��y=��3x+3����A(1��0)��B(0��3)��
��C(0��1)��D(��3��0)�����ֱ��CD�Ľ���ʽΪ��y=![]() x+1�������
x+1�������![]() �ĶԳ���Ϊx=��1��
�ĶԳ���Ϊx=��1��
���Ե�C��E��Q��FΪ������ı�������CEΪһ�ߵ�ƽ���ı��Σ�
��FQ��CE����FQ=CE��
��ֱ��FQ�Ľ���ʽΪ��y=![]() x+b���ߵ�E����C�ĺ��������1��
x+b���ߵ�E����C�ĺ��������1��
���F����Q�ĺ�����Ҳ�����1����|xF��(��1)|=|xF+1|=1�����xF=0��xF=��2��
�ߵ�F��ֱ��![]() ��y=��2x+4�ϣ�
��y=��2x+4�ϣ�
���F����Ϊ(0��3)��(��2��9)��
��F(0��3)����ֱ��FQΪ��y=![]() x+3��
x+3��
��x=��1ʱ��y=![]() ����Q1(��1��
����Q1(��1��![]() ).
).
��F(��2��9)����ֱ��FQΪ��![]() ��
��
��x=��1ʱ��y= ![]() ����Q2(��1��
����Q2(��1��![]() )��
)��
�����������ĵ�Q��2�������ͼ1��ʾ����Q����ΪQ1(��1��![]() )��Q2(��1��
)��Q2(��1��![]() )��
)��
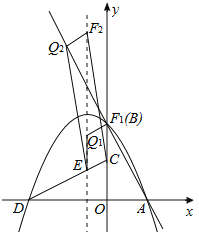
(3)��ͼ2��ʾ������OG��OH���ߵ�G��HΪб���е㣬
��OG=![]() AB��OH=
AB��OH=![]() CD��
CD��
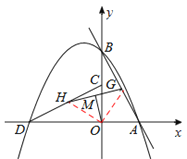
����ת���ʿ�֪��AB=CD��OG��OH��
���OGHΪ����ֱ�������Σ�
�ߵ�GΪGH�е㣬
����OMGΪ����ֱ��������.
��OG=![]() OM=
OM=![]()
![]() =
=![]() .
.
��AB=2OG=![]() ��
��
��![]() ��y=mx+1��
��y=mx+1��
��A(![]() ��0)��B(0��1)��
��0)��B(0��1)��
��Rt��AOB�У��ɹ��ɶ����ã�OA2+OB2=AB2������(![]() )2+12=(
)2+12=(![]() )2��
)2��
��ã�m=��3��m=3.
�ߵ�B��y�������ᣬ
��m=3��ȥ��
��m=��3��
��![]() ��ʾ�ĺ�������ʽΪ��y=��3x+1��
��ʾ�ĺ�������ʽΪ��y=��3x+1��
��B(0��1)��D(��1��0)����A(![]() ��0)��
��0)��
���ô���ϵ�������![]() ��y=��3x2��2x+1��
��y=��3x2��2x+1��


 ������������ϵ�д�
������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Q�ǻ�AB����AB��Χ�ɵ�ͼ�ε��ڲ���һ���㣬P����AB��һ���㣬����PQ���ӳ�����AB�ڵ�C������BC����֪AB��6cm����A��P�����ľ���Ϊxcm��P��C�����ľ���Ϊy1cm��A��C�����ľ���Ϊy2cm��
С������ѧϰ�����ľ��飬�ֱ�Ժ���y1��y2�����Ա���x�ı仯���仯�Ĺ��ɽ�����̽����
������С����̽�����̣��벹��������
��1��ȷ���Ա���x��ȡֵ��Χ�� ��
��2�����±����Ա���x��ֵ����ȡ�㡢��ͼ���������ֱ�õ���y1��y2��x�ļ����Ӧֵ��
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 5.62 | 4.67 | 3.76 | 2.65 | 3.18 | 4.37 | |
y2/cm | 5.62 | 5.59 | 5.53 | 5.42 | 5.19 | 4.73 | 4.11 |
��3����ͬһƽ��ֱ������ϵxOy�У������ȫ��ı��и�����ֵ����Ӧ�ĵ㣨x��y1������x��y2�������������y1��y2��ͼ��
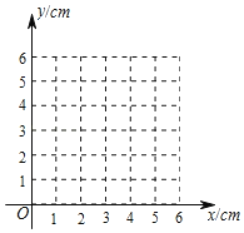
��4����Ϻ���ͼ������⣺����APCΪ����������ʱ��AP�ij���ԼΪ cm��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
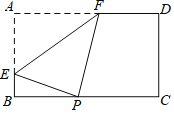
����Ŀ����ͼ����ֽƬABCD�У�![]() ��
��![]() ��P�DZ�BC�ϵĶ��㣬�ֽ�ֽƬ�۵���ʹ��A���P�غϣ��ۺ�����αߵĽ���ֱ���E��F��Ҫʹ�ۺ�ʼ�����AB��AD�н��㣬��BP��ȡֵ��Χ��______��
��P�DZ�BC�ϵĶ��㣬�ֽ�ֽƬ�۵���ʹ��A���P�غϣ��ۺ�����αߵĽ���ֱ���E��F��Ҫʹ�ۺ�ʼ�����AB��AD�н��㣬��BP��ȡֵ��Χ��______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
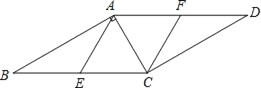
����Ŀ����ͼ����֪��E��F�ֱ���ABCD�ı�BC��AD�ϵ��е㣬����BAC=90��������B=30�㣬BC=10�����ı���AECF�����Ϊ__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�ڵĵ�M����ᡢ�����궼Ϊ��������ѵ�M�����������������磺P(1��0)��Q(2����2)��������������������y��mx2��4mx+4m-2(m![]() 0)��x�ύ�ڵ�A��B���㣬������������A��B֮��IJ������߶�AB��Χ�ɵ�����(�����߽�)ǡ���߸����㣬��m��ȡֵ��Χ��( )
0)��x�ύ�ڵ�A��B���㣬������������A��B֮��IJ������߶�AB��Χ�ɵ�����(�����߽�)ǡ���߸����㣬��m��ȡֵ��Χ��( )
A. ![]() <m��1B.
<m��1B. ![]() ��m<1C. 1<m��2D. 1<m<2
��m<1C. 1<m��2D. 1<m<2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
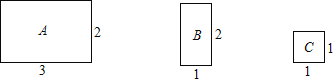
����Ŀ����ͼ�е�A�͡�B�͡�C�;���ֽƬ�ֱ����3�������У����ӵ���״����С���ʵض���ͬ���ٽ���3������װ��һֻ�����Ĵ����У�
��1�����Ⱥ��������1�����ӣ��������ĺ�������![]() �;���ֽƬ�ĸ��ʣ�
�;���ֽƬ�ĸ��ʣ�
��2�����Ⱥ��ȴ�������1�����ӣ����Żأ����ٴ����µ���������������һ�����ӣ���2�������ĺ��ӵ�ֽƬ��ƴ��һ���¾��εĸ��ʣ����ص���϶ƴ�ӣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
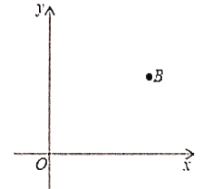
����Ŀ����ͼ��ƽ��ֱ������ϵ�У���֪��![]() ������Ϊ
������Ϊ![]() .
.
��1������ֱ�ߣ������̶ȣ���Բ����һ��ֱ��![]() ������
������![]() ���
���![]() ���������ֱ��ڵ�
���������ֱ��ڵ�![]() �͵�
�͵�![]() ����
����![]() ��
��![]() ����ֱ��
����ֱ��![]() �Գ�.����ͼ����д��������Ҫ������ͼ�ۼ�.��
�Գ�.����ͼ����д��������Ҫ������ͼ�ۼ�.��
��2���������1����������ֱ��![]() �ĺ�������ʽ.
�ĺ�������ʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
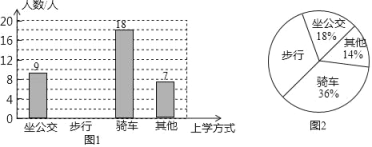
����Ŀ�� ������ѧУ����Խ��Խ�࣬���ֺ������ܾͽ���ѧ��ij��ѧѧϰ��ȤС����꼶��1����ѧ����ѧ�Ľ�ͨ��ʽ�����ʾ����飬������������������������������ͳ��ͼ��ͼ1��ͼ2���������ͼ�е���Ϣ����������⣮
��1���ð���뱾���ʾ������ѧ�����ж����ˣ�
��2���벹ȫͼ1�е�����ͳ��ͼ��
��3����ͼ2������ͳ��ͼ�У����ﳵ���������ε�Բ�ĽǵĶ����Ƕ��ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l����A(6��0)��B(0��12)���㣬����ֱ��y��x���ڵ�C����P(m��0)��x�����˶���
(1)��ֱ��l�Ľ���ʽ��
(2)����P��l��ƽ���߽�ֱ��y��x�ڵ�D����m��3ʱ�����PCD�������
(3)�Ƿ���ڵ�P��ʹ�á�PCA��Ϊ���������Σ������ڣ���ֱ��д�����з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com