
����Ŀ������ѧ��У�С�����ֽ����鲻ͬ�ĵ���ֱ�����ǰ������ת���ܵõ�һ����ۣ�������һ�����ǰ�Rt��ABC��AB��BC��4����BΪֱ�ǣ�����һ�����ֱ�����ǰ��ֱ�Ƕ������б��AC���е�O���������ǰ��Ƶ�O��ת�����ǰ����ֱ�DZ߷ֱ�AB��BC�����ӳ�����E��F���㣬��ͼ����������ת���ǰ�����ͼ�ε����������
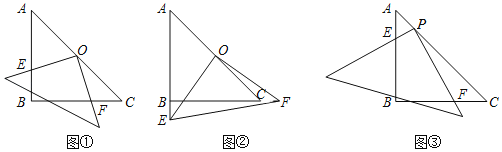
��1�����ǰ��Ƶ�O��ת����OFC�Ƿ��ܳ�Ϊ����ֱ�������Σ����ܣ����CF�������ܣ���˵�����ɣ�
��2�����ǰ��Ƶ�O��ת���߶�OE��OF֮����ʲô������ϵ����ͼ������֤����
��3���������ǰ��ֱ��ԭ�����б���ϵĵ�P������ͼ��������![]() ��PF��PE��������������ϵ��֤���㷢�ֵĽ��ۣ�
��PF��PE��������������ϵ��֤���㷢�ֵĽ��ۣ�
���𰸡���1��CF��2��CF��4����2��OE��OF�����������������3��PF��4PE�������������.
��������
��OFC�ܳ�Ϊ����ֱ�������Σ�����OFC��90������COF��90�����������FC�ij����ɣ���2��OE��OF������OB��CF��������֪������֤OB��OC����EBO=��OCF=135�㡢��EOB����FOC������ASA֤����OEB�ա�OFC�����ɵ�OE=OF����3��PF��4PE����ͼ��������P��PM��AB��M��PN��BC��N��֤����PME�ס�PNF����APM�ס�PCN���������������ε����ʿɵ�![]() ���ɴ˼������
���ɴ˼������![]() �����۵�֤.
�����۵�֤.
�⣺��1����OFC�ܳ�Ϊ����ֱ�������Σ�
��Rt��ABC��AB��BC��4��
���C��45�㣬
�ߡ�OFC�ǵ���ֱ�������Σ�
���OFC��90����COF��90�㣬
����OFC��90��ʱ��OF��BC��
�ߡ�B��90�㣬
��OF��AB��
�ߵ�O��AC���е㣬
���F��BC���е㣬
��CF��![]() BC��2��
BC��2��
����COF��90��ʱ����ʱ��F�͵�B�غϣ�CF��BC��4��
����CF��2��CF��4��
��2��OE��OF��
���ɣ�����OB��CF����ͼ����
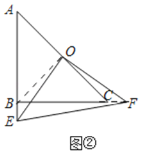
��AB��BC����ABC��90�㣬O��ΪAC���е㣬
��OB��![]() AC��OC����BOC��90������ABO=��ACB=45�㣬
AC��OC����BOC��90������ABO=��ACB=45�㣬
���EBO=��OCF=135�㣮
�ߡ�EOF��90�㣬
���EOB����FOC��
�ڡ�OEB�͡�OFC�У�
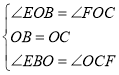 ��
��
���OEB�ա�OFC��
��OE=OF��
��3��PF��4PE����ͼ��������P��PN��AB��N��PM��BC��M��
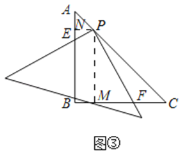
�ߡ�B��90�㣬
���MPN��90�㣬
�ߡ�EPF��90�㣬
���EPN����FPM��
�ߡ�ENP����FMP��90�㣬
���PNE�ס�PMF��
��![]() ��
��
�ߡ�APN�͡�PCMΪ����ֱ�������Σ�
���APM�ס�PCN��
��![]() ,
,
��![]()
��![]() ��
��
��![]() ��
��
��![]() ��
��
����PF��4PE��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���ʵ��
һ�������龳
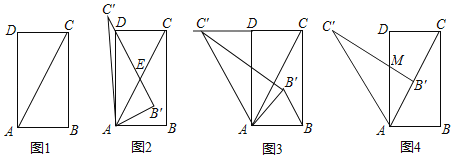
���ۺ���ʵ�����ϣ���ʦ��֯ͬѧ������ֱ�������ε���ת��Ϊ���չ��ѧ�����ͼ1������ABCD�У�AD��2AB������AC������ABC�Ƶ�A��ת��ijһλ�ã��۲�ͼ�Σ�������Ⲣ���Խ����
����ʵ���������������
(1)��ͼ2����˼��ļ�ѧ��ͼ1�еġ�ABC�Ե�AΪ��ת���ģ�����ʱ�뷽����ת���õ���A'B'C'����ʱB'C'����D�����ADB����____�ȣ�
(2)��ѧ���ͬѧ��ͼ2�Ļ����ϼ�����ת��ͼ3����ʱ��C����CD���ӳ����ϣ�����BB'��������������������⣬��������������������������⣮
��C'D��AB�к�������ϵ����˵�����ɣ�
��BB'��AC'�к�λ�ù�ϵ����˵�����ɣ�
(3)��Ӣ���ͬѧ��ͼ3�Ļ����ϰ���ʱ�뷽����ת��AB'��Խ���AC�غ�ʱ��B'C'��AD���ڵ�M����ͼ4����S![]() ��S��ABC��_____��
��S��ABC��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
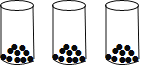
����Ŀ����ͼ��������СͰ��װ��������ͬ��С��(ÿ��СͰ������������С��)��
��һ�α仯�������СͰ���ó�����С������м�СͰ�У�
�ڶ��α仯�����ұ�СͰ���ó�һ��С������м�СͰ�У�
�����α仯�����м�СͰ���ó�һЩС������ұ�СͰ�У�ʹ�ұ�СͰ��С������������������
(1)��ÿ��СͰ��ԭ��3��С�����һ�α仯���м�СͰ��С����������СͰ��С�������____����
(2)��ÿ��СͰ��ԭ��a��С����ڶ��α仯���м�СͰ����_____��С��(��a��ʾ)��
(3)������α仯���м�СͰ���ж��ٸ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
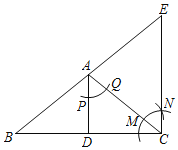
����Ŀ����ͼ���ڡ�ABC�У�ADΪ��BC�ϵ����ߣ���ADƽ�֡�BAC�����ͬѧ������AΪԲ�ģ����ⳤΪ�뾶��������AD�ڵ�P����AC�ڵ�Q��Ȼ���Ե�CΪԲ�ģ�AP��Ϊ�뾶��������AC�ڵ�M������MΪԲ�ģ�PQ��Ϊ�뾶��������ǰ���ڵ�N��������CN����BA���ӳ����ڵ�E��
��1��ͨ����俵���ͼ�����ж�AD��CE��λ�ù�ϵ���� ��������ϵ���� ��
��2����֤��AB��AC��
��3����BC��24��CE��10�����ABC�����ĵ�BC�ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
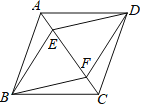
����Ŀ����ͼ��������ABCD�У���E��F�ڶԽ���AC�ϣ���AE��CF��
��1��֤������ABE�ա�ADE��
��2��֤�����ı���BFDE�����Σ�
��3����AC��4![]() ��BD��8��AE��
��BD��8��AE��![]() ��������ı���BFDE�������
��������ı���BFDE�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C��90����BDƽ�֡�ABC����O��AB�ϣ��Ե�OΪԲ�ģ�OBΪ�뾶��Բ������D����BC�ڵ�E
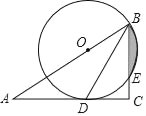
��1����֤��AC�ǡ�O�����ߣ���2����OB��2��CD��![]() ����ͼ����Ӱ���ֵ�������������
����ͼ����Ӱ���ֵ�������������![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ij����֧����һ������¥ǰ����������ϰ����ͼ��ʾ�������ٱ��������ݳɹ��ȳ���C��������ߺ�����C�����Ϸ�17��B������һ������ߣ������ٱ������������ݽ���ȳ�����֪��A�����¥��ˮƽ������15�ף�����A���õ�һ��ʩ��ʱ������ˮƽ�ߵļнǡ�CAD=60�㣬��ڶ���ʩ��ʱ������ˮƽ�ߵļнǡ�BAD�Ķ����������ȷ��1�㣩��
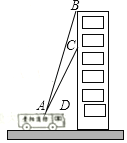
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=��x2+x+6��һ�κ���y=��x+m�����ö��κ�����x���Ϸ���ͼ����x�ᷭ�۵�x���·���ͼ������ಿ�ֲ��䣬�õ�һ���º�������ͼ��ʾ����������ͼ�л��������ͼ��ֱ��y=��x+m����ͼ����4������ʱ��m��ȡֵ��Χ�ǣ�������
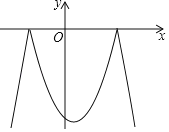
A. ��![]() ��m��3 B. ��
��m��3 B. ��![]() ��m��2 C. ��2��m��3 D. ��6��m����2
��m��2 C. ��2��m��3 D. ��6��m����2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
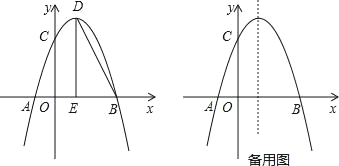
����Ŀ����ͼ��������y=��x2+bx+c��x�ύ�ڵ�A�͵�B��3��0������y�ύ�ڵ�C��0��3������D�������ߵĶ��㣬����D��x��Ĵ��ߣ�����ΪE������DB��
��1����������ߵĽ���ʽ������D�����ꣻ
��2����M���������ϵĶ��㣬���M�ĺ�����Ϊm��
������MBA=��BDEʱ�����M�����ꣻ
������M��MN��x�ᣬ�������߽��ڵ�N��PΪx����һ�㣬����PM��PN������PMN����MN���ۣ�����QMN�����ı���MPNQǡ��Ϊ�����Σ�ֱ��д��m��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com