
【题目】如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E
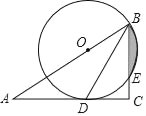
(1)求证:AC是⊙O的切线;(2)若OB=2,CD=![]() ,求图中阴影部分的面积(结果保留
,求图中阴影部分的面积(结果保留![]() ).
).
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,AB=4,点F,C是⊙O上两点,连接AC,AF,OC,弦AC平分∠FAB,∠BOC=60°,过点C作CD⊥AF交AF的延长线于点D,垂足为点D.
(1)求扇形OBC的面积(结果保留π);
(2)求证:CD是⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接2011年高中招生考试,某中学对全校九年级学生进行了一次数学摸底考试,并随机抽取了部分学生的测试成绩作为样本进行,绘制成了如下两幅不完整的统计图,请根据图中所给信息,下列问题:
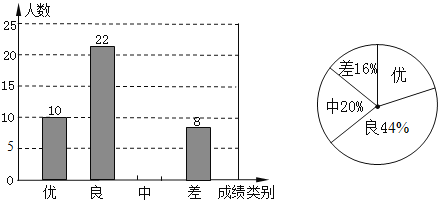
(1)请将表示成绩类别为“中”的条形统计图补充完整;
(2)在扇形统计图中,表示成绩类别为“优”的扇形所对应的圆心角是 72 度;
(3)学校九年级共有1000人参加了这次数学考试,估算该校九年级共有多少名学生的数学成绩可以达到优秀?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初二年級教师对试卷讲评课中学生参与的深度与广度进行评价调査,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初二学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:
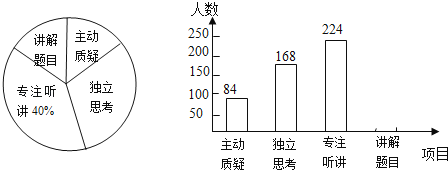
(1)在这次评价中,一共抽査了 名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为 度;
(3)请将频数分布直方图补充完整:
(4)如果全市有30000名初二学生,那么在试卷评讲课中,请估计“独立思考”的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动中,小明发现将两块不同的等腰直角三角板进行旋转,能得到一组结论:在其中一块三角板Rt△ABC,AB=BC=4,∠B为直角,将另一块等腰直角三角板的直角顶点放在斜边AC的中点O处,将三角板绕点O旋转,三角板的两直角边分别交AB、BC或其延长线于E、F两点,如图①与②是旋转三角板所得图形的两种情况.
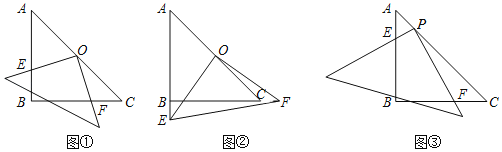
(1)三角板绕点O旋转,△OFC是否能成为等腰直角三角形?若能,求出CF;若不能,请说明理由;
(2)三角板绕点O旋转,线段OE和OF之间有什么数量关系?用图②加以证明;
(3)若将三角板的直角原点放在斜边上的点P处(如图③),当![]() ,PF和PE有怎样的数量关系,证明你发现的结论.
,PF和PE有怎样的数量关系,证明你发现的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |

(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么? (参考数据:三人成绩的方差分别为![]() 、
、![]() 、
、![]() )
)
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
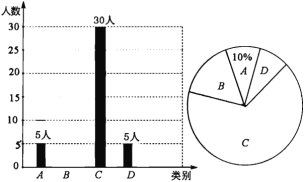
【题目】央视“经典咏流传”开播以来受到社会广泛关注.我市某校就“中华文化我传承——地方戏曲进校园”的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两副尚不完整的统计图.请你根据统计图所提供的信息解答下列问题:
图中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”.
(1)被调查的总人数是_____________人,扇形统计图中C部分所对应的扇形圆心角的度数为_______.
(2)补全条形统计图;
(3)若该校共有学生1800人,请根据上述调查结果,估计该校学生中A类有__________人;
(4)在抽取的A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树形图或列表法求出被抽到的两个学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行“行动起来,对抗雾霾”为主题的植树活动,某街道积极响应,决定对该街道进行绿化改造,共购进甲、乙两种树共50棵,已知甲树每棵800元,乙树每棵1200元.
(1)若购买两种树的总金额为56000元,求甲、乙两种树各购买了多少棵?
(2)若购买甲树的金额不少于购买乙树的金额,至少应购买甲树多少棵?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com