
����Ŀ�������꼉��ʦ���Ծ���������ѧ�������������Ƚ������۵��ˣ���������ĿΪ�������ɡ�����˼����רע������������Ŀ��������������ȡ������������ѧ���IJ�����������Ƴ���ͼ��ʾ��Ƶ���ֲ�ֱ��ͼ������ͳ��ͼ�������������������ͼ��������Ϣ����������⣺
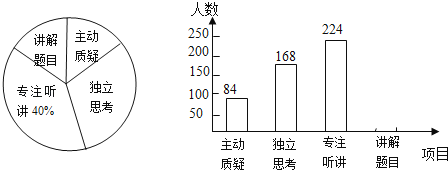
��1������������У�һ��������� ����ѧ����
��2��������ͳ��ͼ�У���Ŀ���������ɡ����ڵ����ε�Բ�ĽǵĶ���Ϊ�� ���ȣ�
��3���뽫Ƶ���ֲ�ֱ��ͼ����������
��4�����ȫ����30000������ѧ������ô���Ծ��������У�����ơ�����˼������Լ�ж����ˣ�
���𰸡���1��560����2��54����3�������������4��9000.
��������
��1������רע������������������ռ�İٷֱȼ��������ε������������2������360������������ɵ�������ռ�İٷֱȼ�����⣻��3����ý�����Ŀ����������ȫͳ��ͼ���ɣ���4���������������Զ���˼��������ռ�İٷֱȼ������.
��1��������������ǣ�224��40%��560���ˣ���
�ʴ��ǣ�560��
��2�����������ɡ����ڵ����ε�Բ�ĽǵĶ����ǣ�360���![]() ��54�㣬
��54�㣬
�ʴ��ǣ�54��
��3����������Ŀ���������ǣ�560��84��168��224��84���ˣ���
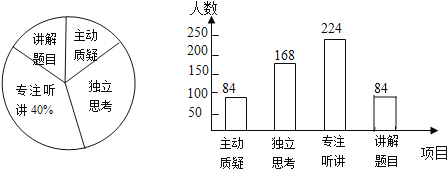 ��
��
��4�����Ծ��������У�������˼�����ij���ѧ��Լ�У�30000��![]() ��9000���ˣ���
��9000���ˣ���


 �¿α�������������ҵ�������γ�����ϵ�д�
�¿α�������������ҵ�������γ�����ϵ�д� ����ν����Ž̲��㽭���̴�ѧ������ϵ�д�
����ν����Ž̲��㽭���̴�ѧ������ϵ�д� �����Ļ������������������ϵ�д�
�����Ļ������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һЩ��С��ȵ�С��������ɵļ����������ͼ������ͼ��ͬ��ͼ��ʾ�����������������С�������������Ϊm�����Ϊn������m��n��ֵ�ֱ�Ϊij�����������ε������߳�����õ��������ε��ܳ�Ϊ( )

A. 11��13B. 13��14C. 13D. 12��13��14��15
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��x�ύ�ڵ�A��B���㣨��A�ڵ�B��ߣ�����y�ύ�ڵ�C��
��x�ύ�ڵ�A��B���㣨��A�ڵ�B��ߣ�����y�ύ�ڵ�C��
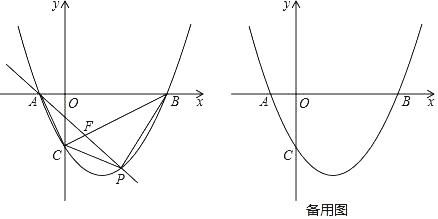
��1����A��B��������꣮
��2����P���߶�BC�·����������ϵĶ��㣬����PC��PB��
���Ƿ����һ��P��ʹ��PBC�������������ڣ��������PBC�����������������ڣ���˵�����ɣ�
������AC��AP��AP��BC�ڵ�F������CAP����ABCʱ����ֱ��AP�ĺ�������ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������ͬѧ�ֱ����6�����ѵ����ѵ���ɼ�����λ���������±�
��һ�� | �ڶ��� | ������ | ���Ĵ� | ����� | ������ | |
�� | 9 | 8 | 6 | 7 | 8 | 10 |
�� | 8 | 7 | 9 | 7 | 8 | 8 |
�����ǵ�ѵ���ɼ������·���������˵����ȷ���ǣ�������
A. ����ѵ���ɼ���ƽ������ͬ B. ����ѵ���ɼ�����λ����ͬ
C. ����ѵ���ɼ���������ͬ D. ����ѵ���ɼ��ķ��ͬ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
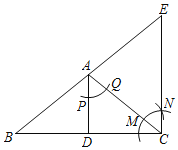
����Ŀ����ͼ���ڡ�ABC�У�ADΪ��BC�ϵ����ߣ���ADƽ�֡�BAC�����ͬѧ������AΪԲ�ģ����ⳤΪ�뾶��������AD�ڵ�P����AC�ڵ�Q��Ȼ���Ե�CΪԲ�ģ�AP��Ϊ�뾶��������AC�ڵ�M������MΪԲ�ģ�PQ��Ϊ�뾶��������ǰ���ڵ�N��������CN����BA���ӳ����ڵ�E��
��1��ͨ����俵���ͼ�����ж�AD��CE��λ�ù�ϵ���� ��������ϵ���� ��
��2����֤��AB��AC��
��3����BC��24��CE��10�����ABC�����ĵ�BC�ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ������D��E����O�ϣ���B��2��ADE����C��BA���ӳ����ϣ�
��������C����DAB����֤��CE����O�����ߣ�
������OF��2��AF��3����EF�ij���
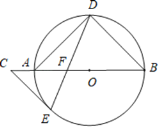
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C��90����BDƽ�֡�ABC����O��AB�ϣ��Ե�OΪԲ�ģ�OBΪ�뾶��Բ������D����BC�ڵ�E
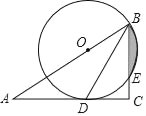
��1����֤��AC�ǡ�O�����ߣ���2����OB��2��CD��![]() ����ͼ����Ӱ���ֵ�������������
����ͼ����Ӱ���ֵ�������������![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵��ϰ�������A��B�����ͺŵ�����100ֻ����֪A�ͺ��������ÿֻ40Ԫ��B�ͺ��������ÿֻ60Ԫ.
��1�����õ��ϰ干������5200Ԫ����ôA��B�ͺ���������˶���ֻ��
��2����B�ͺ���������������A�ͺ�����������![]() ����ô������ֻA�ͺ��������ø��ϰ����õĽ��������٣�
����ô������ֻA�ͺ��������ø��ϰ����õĽ��������٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ1��С�����������У���A��B��C��D������ЩС�������ϣ�AB��CD�ཻ�ڵ�O����tan��AOD���ڣ�������
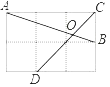
A. ![]() B. 2C. 1D.
B. 2C. 1D. ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com