练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在边长为1的小正方形网格中，点A，B，C，D都在这些小正方形上，AB与CD相交于点O，则tan∠AOD等于（　　）

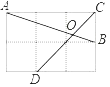
    A. B. 2C. 1D.

    【答案】B

    【解析】

    连接BE，与CD交于点F，根据正方形的性质可得BF＝CF，证明△ACO∽△BHO，根据相似三角形的性质可得HO：CO=BH：AC=1：3，得到

    在Rt△OBF中，求出tan∠BOF==2,即可求出tan∠AOD.

    解：如图，连接BE，与CD交于点F，

    ∵四边形BCEH是正方形，

    ∴，CH=BE，BE⊥CH，

    ∴BF＝CF，

    ∵AC∥BH，

    ∴△ACO∽△BHO，

    ∴HO：CO=BH：AC=1：3，

    ∵CF=HF，

    ∴HO：HF＝1：2，

    ∴

    在Rt△OBF中，tan∠BOF==2,

    ∵∠AOD＝∠BOF，

    ∴tan∠AOD＝2．

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】初二年級教师对试卷讲评课中学生参与的深度与广度进行评价调査，其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项．评价组随机抽取了若干名初二学生的参与情况，绘制成如图所示的频数分布直方图和扇形统计图（均不完整），请根据图中所给信息解答下列问题：

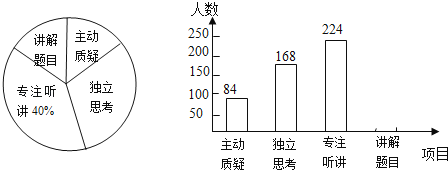
    （1）在这次评价中，一共抽査了　 　名学生；

    （2）在扇形统计图中，项目“主动质疑”所在的扇形的圆心角的度数为　 　度；

    （3）请将频数分布直方图补充完整：

    （4）如果全市有30000名初二学生，那么在试卷评讲课中，请估计“独立思考”的约有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

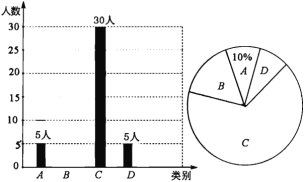
    【题目】央视“经典咏流传”开播以来受到社会广泛关注.我市某校就“中华文化我传承——地方戏曲进校园”的喜爱情况进行了随机调查，对收集的信息进行统计，绘制了下面两副尚不完整的统计图.请你根据统计图所提供的信息解答下列问题：

    图中A表示“很喜欢”，B表示“喜欢”，C表示“一般”，D表示“不喜欢”.

    （1）被调查的总人数是_____________人，扇形统计图中C部分所对应的扇形圆心角的度数为_______.

    （2）补全条形统计图；

    （3）若该校共有学生1800人，请根据上述调查结果，估计该校学生中A类有__________人；

    （4）在抽取的A类5人中，刚好有3个女生2个男生，从中随机抽取两个同学担任两角色，用树形图或列表法求出被抽到的两个学生性别相同的概率.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，AC平分∠BCD，AC⊥AB，E是BC的中点，AD⊥AE．

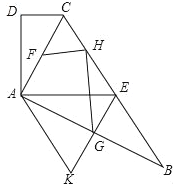
    （1）求证：AC2=CD·BC；

    （2）过E作EG⊥AB，并延长EG至点K，使EK=EB．

    ①若点H是点D关于AC的对称点，点F为AC的中点，求证：FH⊥GH；

    ②若∠B=30°，求证：四边形AKEC是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在2018年“新技术支持未来教育”的教师培训活动中，会议就“面向未来的学校教育、家庭教育及实践应用演示”等问题进行了互动交流，记者随机采访了部分参会教师，对他们发言的次数进行了统计，并绘制了不完整的统计表和条形统计图．

    组别

    发言次数n

    百分比

    A

    0≤n＜3

    10%

    B

    3≤n＜6

    20%

    C

    6≤n＜9

    25%

    D

    9≤n＜12

    30%

    E

    12≤n＜15

    10%

    F

    15≤n＜18

    m%

    请你根据所给的相关信息，解答下列问题：

    （1）本次共随机采访了　_____　名教师，m=　_____　；

    （2）补全条形统计图；

    （3）已知受访的教师中，E组只有2名女教师，F组恰有1名男教师，现要从E组、F组中分别选派1名教师写总结报告，请用列表法或画树状图的方法，求所选派的两名教师恰好是1男1女的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角（两边足够长），用28m长的篱笆围成一个矩形花园ABCD（篱笆只围AB，BC两边），设AB＝xm，花园的面积为Sm2．

    （1）若花园的面积为192m2，求x的值；

    （2）写出花园面积S与x的函数关系式．x为何值时，花园面积S有最大值？最大值为多少？

    （3）若在P处有一棵树与墙CD，AD的距离分别是a（14≤a≤22）和6m，要将这棵树围在花园内（含边界，不考虑树的粗细），设花园面积S的最大值为y，直接写出y与a的关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市举行“行动起来，对抗雾霾”为主题的植树活动，某街道积极响应，决定对该街道进行绿化改造，共购进甲、乙两种树共50棵，已知甲树每棵800元，乙树每棵1200元．

    （1）若购买两种树的总金额为56000元，求甲、乙两种树各购买了多少棵？

    （2）若购买甲树的金额不少于购买乙树的金额，至少应购买甲树多少棵？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线l1的解析表达式为：y=﹣3x+3，且l1与x轴交于点D，直线l2经过点A、B，直线l1，l2交于点C．

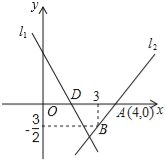
    （1）求点D的坐标；

    （2）求直线l2的解析表达式；

    （3）求△ADC的面积；

    （4）在l2上存在异于点C的另一点P，使得△ADP与△ADC面积相等，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

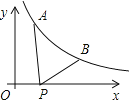
    【题目】如图所示，已知A（，y1），B(2,y2)为反比例函数图像上的两点，动点P(x，0)在x正半轴上运动，当线段AP与线段BP之差达到最大时，点P的坐标是（ ）

    A. (，0) B. (1,0) C. (,0) D. (,0)

    查看答案和解析>>

    同步练习册答案