
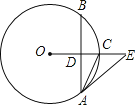
【题目】如图,在⊙O中,半径OC垂直于弦AB,垂足为点D,点E在OC的延长线上,∠EAC=∠BAC
(1)求证:AE是⊙O的切线;
(2)若AB=8,cosE=![]() ,求CD的长.
,求CD的长.
【答案】(1)见解析;(2)CD= 2.
【解析】
(1)连接OA,求出∠AOC=∠BAE,求出∠OAE=90°,根据切线的判定得出即可;
(2)根据垂径定理求出AD,证明△ODA∽△OAE,得到∠OAD=∠E,根据正切的定义计算即可.
(1)证明:连接OA,
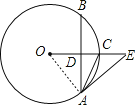
∵AB⊥OC,OC过O,
∴![]() ,
,
∴∠CAB=![]() ∠AOC,
∠AOC,
∵∠EAC=∠BAC,
∴∠EAB=∠AOC,
∵OC⊥AB,
∴∠ODA=90°,
∴∠OAB+∠AOC=90°,
∴∠OAB+∠BAE=90°,
即OA⊥AE,
∵OA过点O,
∴AE是⊙O的切线;
(2)解:∵OD⊥AB,AB=8,
∴AD=![]() AB=4,
AB=4,
∵∠OAE=∠ODA=90°,∠O=∠O,
∴△ODA∽△OAE,
∴∠OAD=∠E,
∵cosE=![]() ,
,
∴cos∠OAD=![]() ,
,
∴OA=5,
∴OD=3,
∴CD=OC-OD=5-3=2.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】二次函数 y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线 x=1,下列结论:①ab<0;②b2>4ac;③a+b+2c<0;④3a+c<0. 其中正确的是( )
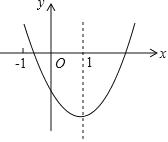
A.①④B.②④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
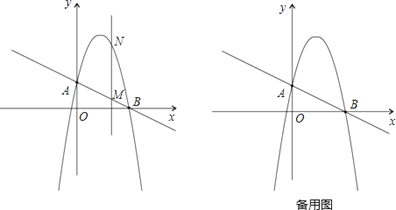
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
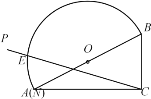
【题目】如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器零刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒4度的速度旋转,CP与量角器的半圆弧交于点E,第18秒时,点E在量角器上对应的读数是__________度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于A(﹣2,0),点B(4,0).

(1)求抛物线的解析式;
(2)若点M是抛物线上的一动点,且在直线BC的上方,当S△MBC取得最大值时,求点M的坐标;
(3)在直线的上方,抛物线是否存在点M,使四边形ABMC的面积为15?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B

(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6![]() ,AF=4
,AF=4![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
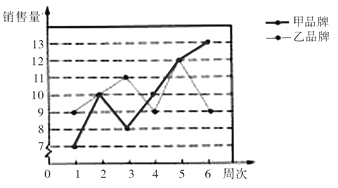
【题目】某家电销售商店1-6周销售甲、乙两种品牌冰箱的数量如图所示(单位:台):
(1)分别求该商店这段时间内甲、乙两种品牌冰箱周销售量的平均数和方差;
(2)根据计算结果及折线统计图,对该商店今后采购这两种品牌冰箱的意向提出建议,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
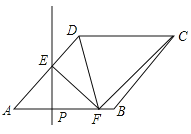
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一动点,且不与点
上一动点,且不与点![]() 重合,过点
重合,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,将
,将![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在直线
落在直线![]() 上点
上点![]() 处,连接
处,连接![]() 、
、![]() ,当
,当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长是_________.
的长是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
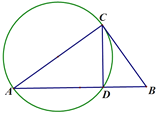
【题目】下面是娜娜设计的“作一个角等于已知角”的尺规作图过程.
已知:RT△ABC,
求作:AB上作点D,使∠BCD=∠A.

作法:如图,以AC为直径作圆,交AB于D,所以点D就是所求作的点;
根据娜娜设计的作图过程,完成下面的证明.
证明:∵AC是直径
∴∠ADC=90°(______)(填推理的依据)
即∠ACD+∠A=90°,
∵∠ACB=90°,
即∠ACD+_______=90°,
∴∠BCD=∠A(_______)(填推理的依据).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com