
【题目】某工程队(有甲、乙两组)承包一条路段的修建工程,要求在规定时间内完成.
(1)已知甲组单独完成这项工作所需时间比规定时间多32天,乙组单独完成这项工程所需时间比规定时间多12,如果甲、乙两组先合作20天,剩下的由甲组单独做,则要误期2天完成,那么规定时间是多少天?
(2)在实际工作中,甲、乙两组合做这项工作的![]() 后,工程队又承包了其他路段的工程,需抽调一组过去,从按时完成任务的角度考虑,你认为留下哪一组最好?请说明理由.
后,工程队又承包了其他路段的工程,需抽调一组过去,从按时完成任务的角度考虑,你认为留下哪一组最好?请说明理由.
【答案】(1)28天;(2)留下乙组最好.
【解析】
(1)先设规定的时间是x天,根据题意列出分式方程,解出x的值,再进行检验即可得出答案;
(2)先设甲、乙两组合作完成这项工程的![]() 用了y天,根据题意找出相等的量,列出方程,求出y的值,再分别求出甲、乙组单独做剩下的工程所需的时间,与原规定的天数进行比较,即可得出留下哪一组最好.
用了y天,根据题意找出相等的量,列出方程,求出y的值,再分别求出甲、乙组单独做剩下的工程所需的时间,与原规定的天数进行比较,即可得出留下哪一组最好.
解:(1)设规定的时间是![]() 天,根据题意得:
天,根据题意得:
![]() ,
,
解得![]() ,经检验
,经检验![]() 是原方程的根,
是原方程的根,
答:规定的时间是28天;
(2)设甲、乙两组合作完成这项工作的![]() 用了
用了![]() 天,根据题意得:
天,根据题意得:
![]() ,
,
解得:![]() ,
,
若甲组单独做剩下的工程所需时间为![]() (天),
(天),
∵![]() ,
,
∴甲组单独做剩下的工程不能在规定的时间内完成,
若乙组单独做剩下的工程所需时间为![]() (天)
(天)
∵![]() ,
,
∴乙组单独做剩下的工程能在规定的时间内完成,
∴留下乙组最好.


科目:初中数学 来源: 题型:
【题目】(本题满分8分)某种电子产品共![]() 件,其中有正品和次品.已知从中任意取出一件,取得的产品为次品的概率为
件,其中有正品和次品.已知从中任意取出一件,取得的产品为次品的概率为![]() .
.
(1)该批产品有正品 件;
(2)如果从中任意取出![]() 件,利用列表或树状图求取出
件,利用列表或树状图求取出![]() 件都是正品的概率.
件都是正品的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
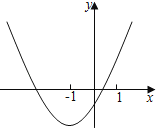
【题目】抛物线y=ax2+bx+c(a≠0)对称轴为直线x=﹣1,其图象如图所示:
![]() a>b>c;
a>b>c;
![]() 4a﹣2b+c<0;
4a﹣2b+c<0;
![]() b2﹣4ac<0;
b2﹣4ac<0;
![]() 3b+2c>0;
3b+2c>0;
![]() m(am+b)+b>a(m是任意实数),其中正确的个数是( )
m(am+b)+b>a(m是任意实数),其中正确的个数是( )
A.3个B.2个C.1个D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
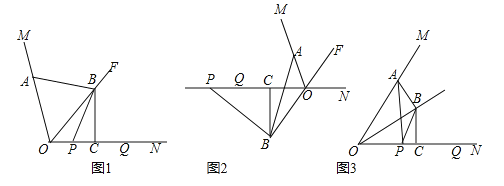
【题目】如图,OF是∠MON的平分线,点A在射线OM上,P,Q是直线ON上的两动点,点Q在点P的右侧,且PQ=OA,作线段OQ的垂直平分线,分别交直线OF、ON交于点B、点C,连接AB、PB.
(1)如图1,当P、Q两点都在射线ON上时,请直接写出线段AB与PB的数量关系;
(2)如图2,当P、Q两点都在射线ON的反向延长线上时,线段AB,PB是否还存在(1)中的数量关系?若存在,请写出证明过程;若不存在,请说明理由;
(3)如图3,∠MON=60°,连接AP,设![]() =k,当P和Q两点都在射线ON上移动时,k是否存在最小值?若存在,请直接写出k的最小值;若不存在,请说明理由.
=k,当P和Q两点都在射线ON上移动时,k是否存在最小值?若存在,请直接写出k的最小值;若不存在,请说明理由.
【答案】(1)AB=PB;(2)存在;(3)k=0.5.
【解析】试题分析:(1)结论:AB=PB.连接BQ,只要证明△AOB≌△PQB即可解决问题;
(2)存在.证明方法类似(1);
(3)连接BQ.只要证明△ABP∽△OBQ,即可推出![]() =
=![]() ,由∠AOB=30°,推出当BA⊥OM时,
,由∠AOB=30°,推出当BA⊥OM时, ![]() 的值最小,最小值为0.5,由此即可解决问题;
的值最小,最小值为0.5,由此即可解决问题;
试题解析:解:(1)连接:AB=PB.理由:如图1中,连接BQ.
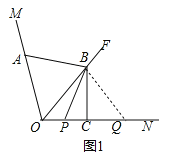
∵BC垂直平分OQ,∴BO=BQ,∴∠BOQ=∠BQO,∵OF平分∠MON,∴∠AOB=∠BQO,∵OA=PQ,∴△AOB≌△PQB,∴AB=PB.
(2)存在,理由:如图2中,连接BQ.
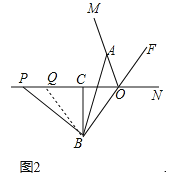
∵BC垂直平分OQ,∴BO=BQ,∴∠BOQ=∠BQO,∵OF平分∠MON,∠BOQ=∠FON,∴∠AOF=∠FON=∠BQC,∴∠BQP=∠AOB,∵OA=PQ,∴△AOB≌△PQB,∴AB=PB.
(3)连接BQ.

易证△ABO≌△PBQ,∴∠OAB=∠BPQ,AB=PB,∵∠OPB+∠BPQ=180°,∴∠OAB+∠OPB=180°,∠AOP+∠ABP=180°,∵∠MON=60°,∴∠ABP=120°,∵BA=BP,∴∠BAP=∠BPA=30°,∵BO=BQ,∴∠BOQ=∠BQO=30°,∴△ABP∽△OBQ,∴ ![]() =
=![]() ,∵∠AOB=30°,∴当BA⊥OM时,
,∵∠AOB=30°,∴当BA⊥OM时, ![]() 的值最小,最小值为0.5,∴k=0.5.
的值最小,最小值为0.5,∴k=0.5.
点睛:本题考查相似综合题、全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,学会用转化的思想思考问题,属于中考常考题型.
【题型】解答题
【结束】
28
【题目】如图,已知抛物线y=ax2+![]() x+c与x轴交于A,B两点,与y轴交于丁C,且A(2,0),C(0,﹣4),直线l:y=﹣
x+c与x轴交于A,B两点,与y轴交于丁C,且A(2,0),C(0,﹣4),直线l:y=﹣![]() x﹣4与x轴交于点D,点P是抛物线y=ax2+
x﹣4与x轴交于点D,点P是抛物线y=ax2+![]() x+c上的一动点,过点P作PE⊥x轴,垂足为E,交直线l于点F.
x+c上的一动点,过点P作PE⊥x轴,垂足为E,交直线l于点F.
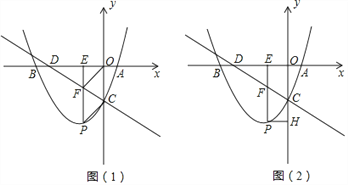
(1)试求该抛物线表达式;
(2)如图(1),若点P在第三象限,四边形PCOF是平行四边形,求P点的坐标;
(3)如图(2),过点P作PH⊥y轴,垂足为H,连接AC.
①求证:△ACD是直角三角形;
②试问当P点横坐标为何值时,使得以点P、C、H为顶点的三角形与△ACD相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知抛物线的顶点为A(2,![]() ),抛线物与y轴交于点B(0,
),抛线物与y轴交于点B(0,![]() ),点C在其对称轴上且位于点A下方,将线段AC绕点C按顺时针方向旋转90°,点A落在抛物线上的点P处.
),点C在其对称轴上且位于点A下方,将线段AC绕点C按顺时针方向旋转90°,点A落在抛物线上的点P处.
(1)求抛物线的解析式;
(2)求线段AC的长;
(3)将抛物线平移,使其顶点A移到原点O的位置,这时点P落在点D的位置,如果点M在y轴上,且以O,C,D,M为顶点的四边形的面积为8,求点M的坐标.
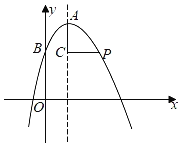
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)2019年4月28日,由世界月季联合会中国花卉协会中国花卉协会月季分会主办的“2019世界月季洲际大会暨第九届中国月季展”在河南南阳开幕.来自澳大利亚比利时智利芬兰等18个国家的专家学者和其他各界人士共襄盛会,交流月季栽培造景育种文化等方面的研究进展及成果.为了解该市市民对月季展的关注情况(选项分为:“A—高度关注”,“B—一般关注”,“C—关注度低”,“D—不关注”),某校兴趣小组随机采访该市部分市民,对采访情况制作了如下不完整的统计图表.
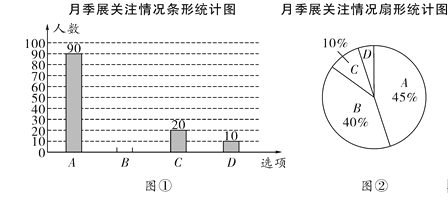
根据以上统计图,解答下列问题:
(1)本次接受采访的市民共有________人;
(2)在扇形统计图中,扇形D的圆心角的度数是_________;
(3)请补全条形统计图;
(4)若该市区有100万人,根据采访结果,估计不关注月季展市民的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果

下面有三个推断:
①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;
②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;
③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.
其中合理的是( )
A.①B.②C.①②D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两同学从![]() 地出发,骑自行车在同一条路上行驶到
地出发,骑自行车在同一条路上行驶到![]() 地,他们离出发地的距离为
地,他们离出发地的距离为![]() 和行驶时间
和行驶时间![]() 之间的函数关系的图像如图所示,则下列结论错误的是( )
之间的函数关系的图像如图所示,则下列结论错误的是( )
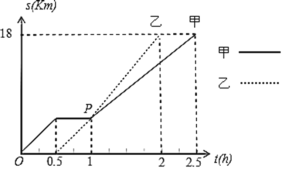
A.![]() 、
、![]() 两地相距
两地相距![]() B.甲在途中停留了0.5小时
B.甲在途中停留了0.5小时
C.全程乙比甲少用了1小时D.乙出发后0.5小时追上甲
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在平面直角坐标系中,点A的坐标为(6,![]() ),AB⊥x轴于点B,AC⊥y轴于点C,连接BC.点D是线段AC的中点,点E的坐标为(0,
),AB⊥x轴于点B,AC⊥y轴于点C,连接BC.点D是线段AC的中点,点E的坐标为(0,![]() ),点F是线段EO上的一个动点.过点A,D,F的抛物线与x轴正半轴交于点G,连接DG交线段AB于点M.
),点F是线段EO上的一个动点.过点A,D,F的抛物线与x轴正半轴交于点G,连接DG交线段AB于点M.
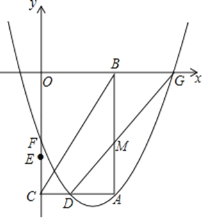
(1)求∠ACB的度数;
(2)当点F运动到原点时,求过A,D,F三点的抛物线的函数表达式及点G的坐标;
(3)以线段DM为一边作等边三角形DMP,点P与点A在直线DG同侧,当点F从点E运动到点O时,请直接写出点P运动的路径的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com