
����Ŀ�� ��ͼ����ƽ��ֱ������ϵ�У���A������Ϊ��6��![]() ����AB��x���ڵ�B��AC��y���ڵ�C������BC����D���߶�AC���е㣬��E������Ϊ��0��
����AB��x���ڵ�B��AC��y���ڵ�C������BC����D���߶�AC���е㣬��E������Ϊ��0��![]() ������F���߶�EO�ϵ�һ�����㣮����A��D��F����������x�������ύ�ڵ�G������DG���߶�AB�ڵ�M��
������F���߶�EO�ϵ�һ�����㣮����A��D��F����������x�������ύ�ڵ�G������DG���߶�AB�ڵ�M��
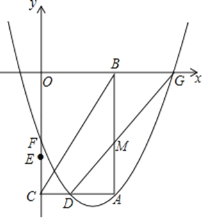
(1)���ACB�Ķ�����
(2)����F�˶���ԭ��ʱ�����A��D��F����������ߵĺ�������ʽ����G�����ꣻ
(3)���߶�DMΪһ�����ȱ�������DMP����P���A��ֱ��DGͬ�࣬����F�ӵ�E�˶�����Oʱ����ֱ��д����P�˶���·���ij���
���𰸡�(1)![]() (2)
(2)![]()
![]() (3)
(3)![]()
��������
��1����ȷ����AB��AC�����жϳ���BAC��90�㣬�����������Ǻ������ɵó����ۣ�
��2����ȷ������C�����꣬����ȷ������D�����꣬����ô���ϵ���������ɵó����ۣ�
��3�����жϳ���F�ӵ�E�˶�����Oʱ����M���˶��켣��MM'�������жϳ���P���˶��켣�����жϳ���MDM'�ա�PDP'�����ֱ��BG�Ľ���ʽ�����������M�����꣬���ɵó����ۣ�
�⣺��1���ߵ�A������Ϊ![]() ��AB��x���ڵ�B��
��AB��x���ڵ�B��
��B��6��0����
��AB��![]() ��
��
�ߵ�A������Ϊ![]() ��AC��y���ڵ�C��
��AC��y���ڵ�C��
��C��0��![]() ����
����
��AC��6��
��AB��x�ᣬAC��y�ᣬ
���ABO����ACO��90�㣽��BOC��
���ı���OBAC�Ǿ��Σ�
���BAC��90�㣬
��Rt��ABC��tan��ACB��![]() ��
��
���ACB��60�㣻
��2���ɣ�1��֪��C��0��![]() ����
����
�ߵ�D��AC���е㣬
��D��3��![]() ����
����
�������ߵĽ���ʽΪy��ax2+bx+c��
����A��6��![]() ����D��3��
����D��3��![]() ����O��0��0�����������߽���ʽ�У���
����O��0��0�����������߽���ʽ�У���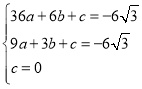 ��
��
��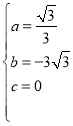 ��
��
�������ߵĽ���ʽΪ![]() ��
��
��y��0����![]() ��
��
��x��0��x��9��
��G��9��0����
��3����ͼ��
����F�ӵ�E�˶�����Oʱ����M���˶��켣���߶�MM'��
����DMΪ�ߵĵȱ������εĶ���P�Ĺ켣���߶�PP'��
�������߹�ԭ��ʱ��DG��AB�Ľ��������M���������߹���Eʱ��DG'��AB�Ľ���ΪM'��
�ߡ�DMP�ǵȱ������Σ�
��DM��DP����MDP��60�㣬
�ߡ�DM'P'�ǵȱ�������
��DM'��DP'����M'DP'��60�㣬
���MDM'����PDP'��
���MDM'�ա�PDP'��SAS����
��PP'��MM'��
�ɣ�2��֪��G��9��0����
��D��3��![]() ����
����
��ֱ��DG�Ľ���ʽ![]() ��
��
��x��6����y��![]() ��
��
��M![]() ��
��
�������߹���Eʱ���������߹���A��D��E��
�������ߵĽ���ʽΪ![]() ��
��
��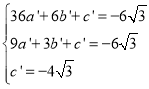 ��
��
��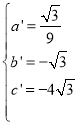 ��
��
�����A��D��E�������ߵĽ���ʽΪ![]() ��
��
��y��0����![]() ��
��
��x����3��x��12��
��G'��12��0����
��DG'�Ľ���ʽΪ![]() ��
��
��x��6����y��![]() ��
��
��M'��6��![]() ����
����
��PP'��MM'��![]() ��
��
����P�˶���·���ij�Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���̶ӣ��мס������飩�а�һ��·�ε������̣�Ҫ���ڹ涨ʱ������ɣ�
��1����֪���鵥��������������ʱ��ȹ涨ʱ���32�죬���鵥��������������ʱ��ȹ涨ʱ���12������ס��������Ⱥ���20�죬ʣ�µ��ɼ��鵥��������Ҫ����2����ɣ���ô�涨ʱ���Ƕ����죿
��2����ʵ�ʹ����У��ס�����������������![]() ���̶��ֳа�������·�εĹ��̣�����һ���ȥ���Ӱ�ʱ�������ĽǶȿ��ǣ�����Ϊ������һ����ã���˵�����ɣ�
���̶��ֳа�������·�εĹ��̣�����һ���ȥ���Ӱ�ʱ�������ĽǶȿ��ǣ�����Ϊ������һ����ã���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
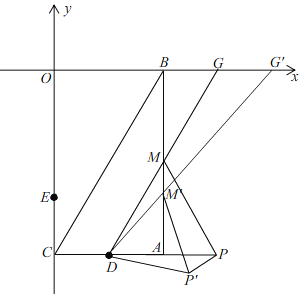
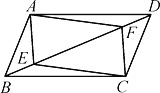
����Ŀ����ͼ������ ABCD�У���E��F�ڶԽ���BD�ϣ���BE��DF.
(1)��֤��AE��CF��
(2)��֤���ı���AECF��ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ž��õĿ��ٷ�չ����������Խ��Խ�ܵ����ǵĹ�ע��ijУѧ����Ϊ���˽���������֪ʶ���ռ��������������˲���ѧ������������Ϊ���dz��˽������˽������˽�����������˽������࣬�������������Ƴ���������ͳ��ͼ��

��1�����α������ѧ���ж���������ȫ����ͳ��ͼ��
��2�����Ƹ�У1200��ѧ�������dz��˽��������˽������������Ƕ��٣�
��3������������dz��˽�����ѧ������2������������ΪŮ�������������ȡ2����ȫУ����������֪ʶ�����������û���״ͼ���б��ķ�������ǡ�ó鵽һ��һŮ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��ͼ���ڡ�ABC�У�DE�DZ�AB�Ĵ�ֱƽ���ߣ��ֱ�AB��AC�ڵ�D��E������BE����F�ڱ�AC�ϣ�AB��AF������BF��
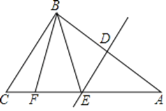
(1)��֤����BEC��2��A��
(2)����BFC��108��ʱ�����A�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ŀڴ��װ�����ɸ���ȫ��ͬ��A��B��C����������A��x����B��x����C��x+1��������������������һ������A��ĸ���Ϊ0.25��
��1���������A��B��C����������ٸ���
��2����С���ӿڴ������ģ��1����Żأ����������1���������û���״ͼ�ķ�����С������1��A���1��C��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳��ٰ�齱����������£��ڲ����Ĵ�������2�������2��������Щ�����ɫ�ⶼ��ͬ���˿�ÿ������һ������������������1�ݽ�Ʒ��������������û�н�Ʒ��
��1�����С��ֻ��һ��������ᣬ��ôС����ý�Ʒ�ĸ���Ϊ����������
��2�����С���������������(�����Ż�)����С�����2�ݽ�Ʒ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
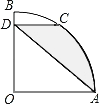
����Ŀ����ͼ��������AOB�У���AOB��90������C��![]() ��
��![]() ��OA��3��CD��OB�ڵ�D����ͼ����Ӱ���ֵ����Ϊ_____��
��OA��3��CD��OB�ڵ�D����ͼ����Ӱ���ֵ����Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
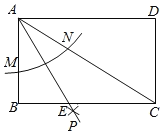
����Ŀ����ͼ������ABCD�С�BAC=60�㣬�Ե�AΪԲ�ģ������ⳤΪ�뾶�����ֱ�AB��AC�ڵ�M��N���㣬�ٷֱ��Ե�M��NΪԲ�ģ��Դ���![]() MN�ij�Ϊ�뾶�������ڵ�P��������AP��BC�ڵ�E����BE=2cm����CE�ij�Ϊ(����)
MN�ij�Ϊ�뾶�������ڵ�P��������AP��BC�ڵ�E����BE=2cm����CE�ij�Ϊ(����)
A.6cmB.6![]() cmC.4cmD.4
cmC.4cmD.4![]() cm
cm
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com