练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在一个不透明的口袋里，装有若干个完全相同的A、B、C三种球，其中A球x个，B球x个，C球（x+1）个．若从中任意摸出一个球是A球的概率为0.25．

    （1）这个袋中A、B、C三种球各多少个？

    （2）若小明从口袋中随机模出1个球后不放回，再随机摸出1个．请你用画树状图的方法求小明摸到1个A球和1个C球的概率．

    【答案】（1）这个袋中A、B、C三种球分别为1个、1个、2个；（2）

    【解析】

    （1）由题意列方程，解方程即可；

    （2）首先画树状图，由概率公式即可得出答案．

    解：由题意得：[x+x+（x+1）]＝x，

    解得：x＝1，∴x+1＝2，

    答：这个袋中A、B、C三种球分别为1个、1个、2个；

    （2）由题意，画树状图如图所示共有12个等可能的结果，摸到1个A球和1个C球的结果有4个，

    ∴摸到1个A球和1个C球的概率为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】(9分)2019年4月28日，由世界月季联合会中国花卉协会中国花卉协会月季分会主办的“2019世界月季洲际大会暨第九届中国月季展”在河南南阳开幕.来自澳大利亚比利时智利芬兰等18个国家的专家学者和其他各界人士共襄盛会，交流月季栽培造景育种文化等方面的研究进展及成果.为了解该市市民对月季展的关注情况(选项分为：“A—高度关注”，“B—一般关注”，“C—关注度低”，“D—不关注”)，某校兴趣小组随机采访该市部分市民，对采访情况制作了如下不完整的统计图表．

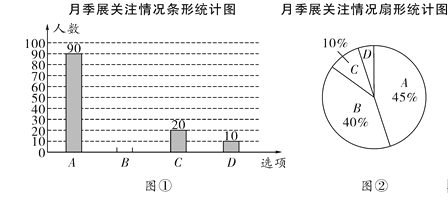
    根据以上统计图，解答下列问题：

    （1）本次接受采访的市民共有________人；

    （2）在扇形统计图中，扇形D的圆心角的度数是_________；

    （3）请补全条形统计图；

    （4）若该市区有100万人，根据采访结果，估计不关注月季展市民的人数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点，交y轴于点C，直线BC的表达式为y=﹣x+3．

    （1）求抛物线的表达式；

    （2）在直线BC上有一点P，使PO+PA的值最小，求点P的坐标；

    （3）在x轴上是否存在一点Q，使得以A、C、Q为顶点的三角形与△BCD相似？若存在，请求出点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 如图，△ABC中，AB＝AC，∠ABC＝α，tanα＝，AD⊥BC于点D，点E是线段AD上的一个动点，连接EB，将线段EB绕点E逆时针旋转2α后得到线段EF，连接AF，若BC＝24，则线段AF的最小值为_____．

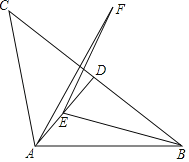
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 如图，在平面直角坐标系中，点A的坐标为（6，），AB⊥x轴于点B，AC⊥y轴于点C，连接BC．点D是线段AC的中点，点E的坐标为（0，），点F是线段EO上的一个动点．过点A，D，F的抛物线与x轴正半轴交于点G，连接DG交线段AB于点M．

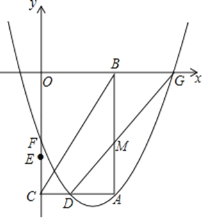
    (1)求∠ACB的度数；

    (2)当点F运动到原点时，求过A，D，F三点的抛物线的函数表达式及点G的坐标；

    (3)以线段DM为一边作等边三角形DMP，点P与点A在直线DG同侧，当点F从点E运动到点O时，请直接写出点P运动的路径的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，AB=2，AD=3．E，F分别是AD，CD上的动点，EF=2．Q是EF的中点，P为BC上的动点，连接AP，PQ．则AP+PQ的最小值等于(　　)

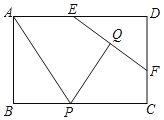
    A.2B.3C.4D.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：对于函数y，我们称函数叫做函数|y|的正值函数．例如：函数y的正值函数为y=||．

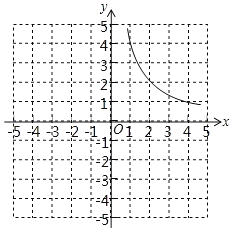
    如图，曲线y(x＞0)请你在图中画出y=x+3的正值函数的图象．

    （1）写出y=x+3的正值函数的两条性质；

    （2）y=x+3的正值函数的图象与x轴、y轴、曲线y(x＞0)的交点分别是A，B，C．点D是线段AC上一动点(不包括端点)，过点D作x轴的平行线，与正值函数图象交于另一点E，与曲线交于点P．

    ①试求△PAD的面积的最大值；

    ②探索：在点D运动的过程中，四边形PAEC能否为平行四边形？若能，求出此时点D的坐标；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某兴趣小组对函数y＝的图象和性质进行探究，请你帮助解决下面问题：

    （1）函数y＝中自变量x的取值范围是　 ；

    （2）如表是x、y的几组对应值，则m＝　 ；

    x

    …

    ﹣2

    ﹣1

    0

    1

    2

    4

    5

    6

    7

    8

    …

    y

    …

    m

    0

    ﹣1

    3

    2

    …

    （3）如图，已经画出了该函数图象的一部分，请你画出函数图象的另一部分；

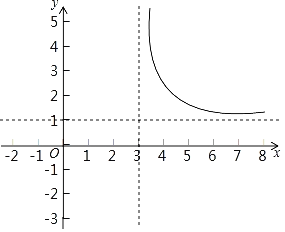
    （4）该函数图象两个分支关于一个点成中心对称，这个点的坐标是　 ；

    （5）若函数y＝的图象上有三点A（x1，y1）、B（x2，y2）、C（x3，y3）且x1＜x2＜3＜x3，则y1、y2、y3的大小关系是　 （用“＜”连接）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

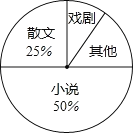
    【题目】东营市某学校九年级一班开展了“读一本好书”的活动，班委会对学生阅读书籍的情况进行了问卷调查，问卷设置了“小说”、“戏剧”、“散文”、“其他”四个类别，每位同学仅选一项，根据调查结果绘制了不完整的频数分布表和扇形统计图．根据图表提供的信息，回答下列问题：

    类别

    频数(人数)

    频率

    小说

    0.5

    戏剧

    4

    n

    散文

    10

    0.25

    其他

    6

    合计

    m

    1

    （1）计算m=　　　　，n=　　　　．

    （2）在扇形统计图中，“其他”类所在的扇形圆心角为　　　　；

    （3）这个学校共有1000人，则读了戏剧类书籍的学生大约有多少人？

    （4）在调查问卷中，甲、乙、丙、丁四位同学选择了“戏剧”类，现从中任意选出2名同学参加学校的戏剧社团，请用画树状图或列表的方法，求选取的2人恰好是乙和丙的概率．

    查看答案和解析>>

    同步练习册答案