
【题目】如图,OF是∠MON的平分线,点A在射线OM上,P,Q是直线ON上的两动点,点Q在点P的右侧,且PQ=OA,作线段OQ的垂直平分线,分别交直线OF、ON交于点B、点C,连接AB、PB.
(1)如图1,当P、Q两点都在射线ON上时,请直接写出线段AB与PB的数量关系;
(2)如图2,当P、Q两点都在射线ON的反向延长线上时,线段AB,PB是否还存在(1)中的数量关系?若存在,请写出证明过程;若不存在,请说明理由;
(3)如图3,∠MON=60°,连接AP,设![]() =k,当P和Q两点都在射线ON上移动时,k是否存在最小值?若存在,请直接写出k的最小值;若不存在,请说明理由.
=k,当P和Q两点都在射线ON上移动时,k是否存在最小值?若存在,请直接写出k的最小值;若不存在,请说明理由.
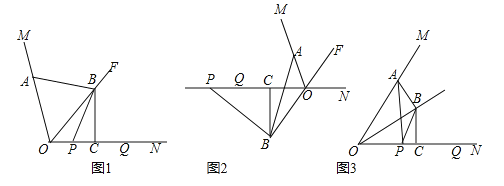
【答案】(1)AB=PB;(2)存在;(3)k=0.5.
【解析】试题分析:(1)结论:AB=PB.连接BQ,只要证明△AOB≌△PQB即可解决问题;
(2)存在.证明方法类似(1);
(3)连接BQ.只要证明△ABP∽△OBQ,即可推出![]() =
=![]() ,由∠AOB=30°,推出当BA⊥OM时,
,由∠AOB=30°,推出当BA⊥OM时, ![]() 的值最小,最小值为0.5,由此即可解决问题;
的值最小,最小值为0.5,由此即可解决问题;
试题解析:解:(1)连接:AB=PB.理由:如图1中,连接BQ.
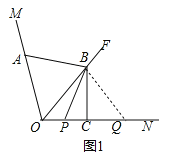
∵BC垂直平分OQ,∴BO=BQ,∴∠BOQ=∠BQO,∵OF平分∠MON,∴∠AOB=∠BQO,∵OA=PQ,∴△AOB≌△PQB,∴AB=PB.
(2)存在,理由:如图2中,连接BQ.
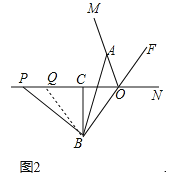
∵BC垂直平分OQ,∴BO=BQ,∴∠BOQ=∠BQO,∵OF平分∠MON,∠BOQ=∠FON,∴∠AOF=∠FON=∠BQC,∴∠BQP=∠AOB,∵OA=PQ,∴△AOB≌△PQB,∴AB=PB.
(3)连接BQ.

易证△ABO≌△PBQ,∴∠OAB=∠BPQ,AB=PB,∵∠OPB+∠BPQ=180°,∴∠OAB+∠OPB=180°,∠AOP+∠ABP=180°,∵∠MON=60°,∴∠ABP=120°,∵BA=BP,∴∠BAP=∠BPA=30°,∵BO=BQ,∴∠BOQ=∠BQO=30°,∴△ABP∽△OBQ,∴ ![]() =
=![]() ,∵∠AOB=30°,∴当BA⊥OM时,
,∵∠AOB=30°,∴当BA⊥OM时, ![]() 的值最小,最小值为0.5,∴k=0.5.
的值最小,最小值为0.5,∴k=0.5.
点睛:本题考查相似综合题、全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,学会用转化的思想思考问题,属于中考常考题型.
【题型】解答题
【结束】
28
【题目】如图,已知抛物线y=ax2+![]() x+c与x轴交于A,B两点,与y轴交于丁C,且A(2,0),C(0,﹣4),直线l:y=﹣
x+c与x轴交于A,B两点,与y轴交于丁C,且A(2,0),C(0,﹣4),直线l:y=﹣![]() x﹣4与x轴交于点D,点P是抛物线y=ax2+
x﹣4与x轴交于点D,点P是抛物线y=ax2+![]() x+c上的一动点,过点P作PE⊥x轴,垂足为E,交直线l于点F.
x+c上的一动点,过点P作PE⊥x轴,垂足为E,交直线l于点F.
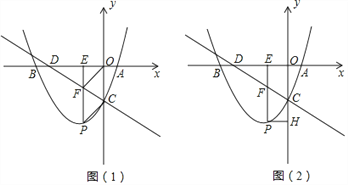
(1)试求该抛物线表达式;
(2)如图(1),若点P在第三象限,四边形PCOF是平行四边形,求P点的坐标;
(3)如图(2),过点P作PH⊥y轴,垂足为H,连接AC.
①求证:△ACD是直角三角形;
②试问当P点横坐标为何值时,使得以点P、C、H为顶点的三角形与△ACD相似?
【答案】(1)y=![]() x2+
x2+![]() x﹣4;(2)点P的坐标为(﹣
x﹣4;(2)点P的坐标为(﹣![]() ,﹣
,﹣![]() )或(﹣8,﹣4);(3)点P的横坐标为﹣5.5或﹣10.5或2或﹣18时,使得以点P、C、H为顶点的三角形与△ACD相似.
)或(﹣8,﹣4);(3)点P的横坐标为﹣5.5或﹣10.5或2或﹣18时,使得以点P、C、H为顶点的三角形与△ACD相似.
【解析】试题分析:(1)利用待定系数法列方程求解析式.(2)把P,F点坐标用m表示写出来,利用四边形PCOF是平行四边形得到m值,求得P点坐标.(3) ①由两点间的距离公式可知分别计算AC,CD,AD勾股定理逆定理知三角形是直角三角形;②分类讨论,△ACD∽△CHP,△ACD∽△PHC分别计算P点坐标.
试题解析:
解:(1)由题意得: 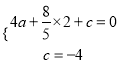 ,解得:
,解得: 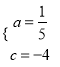 ,
,
∴抛物线的表达式为y=![]() x2+
x2+![]() x﹣4.
x﹣4.
(2)设P(m, ![]() m2+
m2+![]() m﹣4),则F(m,﹣
m﹣4),则F(m,﹣![]() m﹣4).
m﹣4).
∴PF=(﹣![]() m﹣4)﹣(
m﹣4)﹣(![]() m2+
m2+![]() m﹣4)=﹣
m﹣4)=﹣![]() m2﹣
m2﹣![]() m.
m.
∵PE⊥x轴,
∴PF∥OC.
∴PF=OC时,四边形PCOF是平行四边形.
∴﹣![]() m2﹣
m2﹣![]() m=4,解得:m=﹣
m=4,解得:m=﹣![]() 或m=﹣8.
或m=﹣8.
当m=﹣![]() 时,
时, ![]() m2+
m2+![]() m﹣4=﹣
m﹣4=﹣![]() ,
,
当m=﹣8时, ![]() m2+
m2+![]() m﹣4=﹣4.
m﹣4=﹣4.
∴点P的坐标为(﹣![]() ,﹣
,﹣![]() )或(﹣8,﹣4).
)或(﹣8,﹣4).
(3)①证明:把y=0代入y=﹣![]() x﹣4得:﹣
x﹣4得:﹣![]() x﹣4=0,解得:x=﹣8.
x﹣4=0,解得:x=﹣8.
∴D(﹣8,0).
∴OD=8.
∵A(2,0),C(0,﹣4),
∴AD=2﹣(﹣8)=10.
由两点间的距离公式可知:AC2=22+42=20,DC2=82+42=80,AD2=100,
∴AC2+CD2=AD2.
∴△ACD是直角三角形,且∠ACD=90°.
②由①得∠ACD=90°.
当△ACD∽△CHP时, ![]() ,即
,即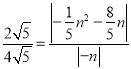 ,
,
解得:n=0(舍去)或n=﹣5.5或n=﹣10.5.
当△ACD∽△PHC时, ![]() ,即
,即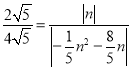 ,
,
解得:n=0(舍去)或n=2或n=﹣18.
综上所述,点P的横坐标为﹣5.5或﹣10.5或2或﹣18时,使得以点P、C、H为顶点的三角形与△ACD相似.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】 (1)问题感知 如图1,在△ABC中,∠C=90°,且AC=BC,点P是边AC的中点,连接BP,将线段PB绕点P顺时针旋转90°到线段PD.连接AD.过点P作PE∥AB交BC于点E,则图中与△BEP全等的三角形是 ,∠BAD= °;
(2)问题拓展 如图2,在△ABC中,AC=BC=![]() AB,点P是CA延长线上一点,连接BP,将线段PB绕点P顺时针旋转到线段PD,使得∠BPD=∠C,连接AD,则线段CP与AD之间存在的数量关系为CP=
AB,点P是CA延长线上一点,连接BP,将线段PB绕点P顺时针旋转到线段PD,使得∠BPD=∠C,连接AD,则线段CP与AD之间存在的数量关系为CP=![]() AD,请给予证明;
AD,请给予证明;
(3)问题解决 如图3,在△ABC中,AC=BC=AB=2,点P在直线AC上,且∠APB=30°,将线段PB绕点P顺时针旋转60°到线段PD,连接AD,请直接写出△ADP的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】武警战士乘一冲锋舟从![]() 地逆流而上,前往
地逆流而上,前往![]() 地营救受困群众,途经
地营救受困群众,途经![]() 地时,由所携带的救生艇将
地时,由所携带的救生艇将![]() 地受困群众运回
地受困群众运回![]() 地,冲锋舟继续前进,到
地,冲锋舟继续前进,到![]() 地接到群众后立刻返回
地接到群众后立刻返回![]() 地,途中曾与救生艇相遇.冲锋舟和救生艇距
地,途中曾与救生艇相遇.冲锋舟和救生艇距![]() 地的距离
地的距离![]() (千米)和冲锋舟出发后所用时间
(千米)和冲锋舟出发后所用时间![]() (分)之间的函数图象如图所示.假设营救群众的时间忽略不计,水流速度和冲锋舟在静水中的速度不变.
(分)之间的函数图象如图所示.假设营救群众的时间忽略不计,水流速度和冲锋舟在静水中的速度不变.

(1)请直接写出冲锋舟从![]() 地到
地到![]() 地所用的时间.
地所用的时间.
(2)求水流的速度.
(3)冲锋舟将![]() 地群众安全送到
地群众安全送到![]() 地后,又立即去接应救生艇.已知救生艇与
地后,又立即去接应救生艇.已知救生艇与![]() 地的距离
地的距离![]() (千米)和冲锋舟出发后所用时间
(千米)和冲锋舟出发后所用时间![]() (分)之间的函数关系式为
(分)之间的函数关系式为![]() ,假设群众上下船的时间不计,求冲锋舟在距离
,假设群众上下船的时间不计,求冲锋舟在距离![]() 地多远处与救生艇第二次相遇?
地多远处与救生艇第二次相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=32°,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:
①AD是∠BAC的平分线;
②CD是△ADC的高;
③点D在AB的垂直平分线上;
④∠ADC=61°.
其中正确的有( ).
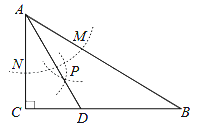
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD,CD,过点D作PD∥BC与AB的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:BD2=PBAC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队(有甲、乙两组)承包一条路段的修建工程,要求在规定时间内完成.
(1)已知甲组单独完成这项工作所需时间比规定时间多32天,乙组单独完成这项工程所需时间比规定时间多12,如果甲、乙两组先合作20天,剩下的由甲组单独做,则要误期2天完成,那么规定时间是多少天?
(2)在实际工作中,甲、乙两组合做这项工作的![]() 后,工程队又承包了其他路段的工程,需抽调一组过去,从按时完成任务的角度考虑,你认为留下哪一组最好?请说明理由.
后,工程队又承包了其他路段的工程,需抽调一组过去,从按时完成任务的角度考虑,你认为留下哪一组最好?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了开展“阳光体育运动”,计划购买篮球、足球共60个,已知每个篮球的价格为70元,每个足球的价格为80元.
(1)若购买这两类球的总金额为4600元,求篮球、足球各买了多少个?
(2)若购买篮球的总金额不超过购买足球的总金额,求最多可购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着经济的快速发展,环境问题越来越受到人们的关注.某校学生会为了了解垃圾分类知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,并将调查结果绘制成下面两幅统计图.

(1)求:本次被调查的学生有多少名?补全条形统计图.
(2)估计该校1200名学生中“非常了解”与“了解”的人数和是多少.
(3)被调查的“非常了解”的学生中有2名男生,其余为女生,从中随机抽取2人在全校做垃圾分类知识交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com