
|
|


科目:初中数学 来源: 题型:
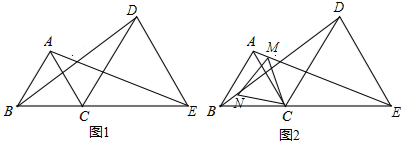
 函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
函数y=x2+bx+c与y=x的图象如图所示,有以下结论:| b2+c2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
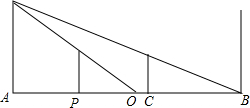 小静晚上从路灯A走向电线杆B,当她走到点P时,发现她影子的顶部刚好接触到路灯A与电线杆B的中点O处;当她再向前走12m到达C点时,发现她影子的顶部刚好接触到电线杆B的底部,已知小静身高1.60m,路灯高4.8m,求路灯A与电线杆B之间的距离.
小静晚上从路灯A走向电线杆B,当她走到点P时,发现她影子的顶部刚好接触到路灯A与电线杆B的中点O处;当她再向前走12m到达C点时,发现她影子的顶部刚好接触到电线杆B的底部,已知小静身高1.60m,路灯高4.8m,求路灯A与电线杆B之间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:
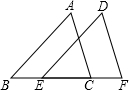 如图所示,在△ABC和△DEF中,B,E,C,F在同一条直线上.已知AC=DF,BE=CF,请你添加一个适当的条件
如图所示,在△ABC和△DEF中,B,E,C,F在同一条直线上.已知AC=DF,BE=CF,请你添加一个适当的条件查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com