
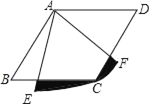
【题目】如图,四边形ABCD是菱形,∠B=60°,AB=1,扇形AEF的半径为1,圆心角为60°,则图中阴影部分的面积是_____.
【答案】![]()
【解析】
根据菱形的性质得出△ADC和△ABC是等边三角形,进而利用全等三角形的判定得出△ADH≌△ACG,得出四边形AGCH的面积等于△ADC的面积,进而求出即可.
连接AC,

∵四边形ABCD是菱形,
∴∠B=∠D=60°,AB=AD=DC=BC=1,
∴∠BCD=∠DAB=120°,
∴∠1=∠2=60°,
∴△ABC、△ADC都是等边三角形,
∴AC=AD=1,
∵AB=1,
∴△ADC的高为![]() ,AC=1,
,AC=1,
∵扇形BEF的半径为1,圆心角为60°,
∴∠4+∠5=60°,∠3+∠5=60°,
∴∠3=∠4,
设AF、DC相交于HG,设BC、AE相交于点G,
在△ADH和△ACG中,
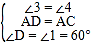 ,
,
∴△ADH≌△ACG(ASA),
∴四边形AGCH的面积等于△ADC的面积,
∴图中阴影部分的面积是:S扇形AEF﹣S△ACD=![]() =
=![]() ,
,
故答案为:![]() .
.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】某科技有限公司用![]() 万元作为新产品的研发费用,成功研制出了一种市场急需的电子产品,已于当年投人生产并进行销售.已知生产这种电子产品的成本为
万元作为新产品的研发费用,成功研制出了一种市场急需的电子产品,已于当年投人生产并进行销售.已知生产这种电子产品的成本为![]() 元/件,在销售过程中发现:每年的年销售量
元/件,在销售过程中发现:每年的年销售量![]() (万件)与销售价格
(万件)与销售价格![]() (元/件)的关系如图所示,其中
(元/件)的关系如图所示,其中![]() 为反比例函数图象的一部分,
为反比例函数图象的一部分,![]() 为一次函数图象的一部分.设公司销售这种电子产品的年利润为
为一次函数图象的一部分.设公司销售这种电子产品的年利润为![]() (万元).(注意:第一年年利润=电子产品销售收人
(万元).(注意:第一年年利润=电子产品销售收人![]() 电子产品生产成本
电子产品生产成本![]() 研发费用)
研发费用)
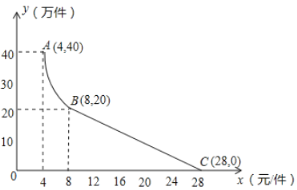
(1)分别写出图中![]() 段、
段、![]() 段
段![]() (万件)与
(万件)与![]() (元/件)之间的函数关系式,并写出自变量的取值范围;
(元/件)之间的函数关系式,并写出自变量的取值范围;
(2)求出第一年这种电子产品的年利润![]() (万元)与
(万元)与![]() (元/件)之间的函数关系式;
(元/件)之间的函数关系式;
(3)求该公司第一年年利润的最大值, 并说明利润最大时是盈利还是亏损,盈利或亏损多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
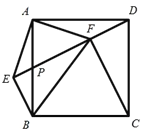
【题目】在正方形 ABCD 中, P 为 AB 的中点,![]() 的延长线于点 E ,连接 AE 、 BE ,
的延长线于点 E ,连接 AE 、 BE ,![]() 交 DP 于点 F ,连接 BF 、FC ,下列结论:①
交 DP 于点 F ,连接 BF 、FC ,下列结论:① ![]() ;② FB AB ;③
;② FB AB ;③ ![]() ;④ FC EF . 其中正确的是( )
;④ FC EF . 其中正确的是( )
A.①②④B.①③④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为初三学生定制校服,对部分学生的服装型号做了调查,结果如下:
型号 | 140 | 150 | 160 | 170 | 180 |
男生 | 11 | 18 | 9 | 7 | 5 |
女生 | 9 | 12 | 18 | 7 | 4 |
下列说法正确的是( )
A.男生服装型号的众数大于女生服装型号的众数
B.男生服装型号的中位数等于女生服装型号的中位数
C.男生服装型号的众数小于女生服装型号的众数
D.男生服装型号的中位数大于女生服装型号的中位数
查看答案和解析>>
科目:初中数学 来源: 题型:
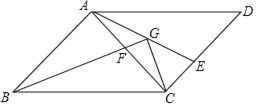
【题目】在平行四边形ABCD中,∠ABC=45°,AB=AC,点E,F分别CD、AC边上的点,且AF=CE,BF的延长线交AE于点G.
(1)若DE=2![]() ,AD=8,求AE.
,AD=8,求AE.
(2)若G是AE的中点,连接CG,求证:![]() AE+CG=BG.
AE+CG=BG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间某商场搞促销活动,方案是:在一个不透明的箱子里放4个完全相同的小球,球上分别标“0元”、“20元”、“30元”、“50元”,顾客每消费满300元,就可从箱子里同时摸出两个球,根据这两个小球所标金额之和可获相应价格的礼品;
(1)若某顾客在甲商商场消费320元,至少可得价值______元的礼品,至多可得价值______元的礼品;
(2)请用画树状图或列表的方法,求该顾客去商场消费,获得礼品的总价值不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
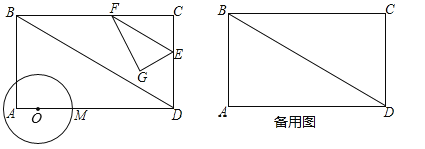
【题目】如图1,已知:在矩形ABCD中,AB![]() cm,AD=9cm,点O从A点出发沿AD以acm/s的速度移向点D移动,以O为圆心,2cm长为半径作圆,交射线AD于M(点M在点O右侧).同时点E从C点出发沿CD以
cm,AD=9cm,点O从A点出发沿AD以acm/s的速度移向点D移动,以O为圆心,2cm长为半径作圆,交射线AD于M(点M在点O右侧).同时点E从C点出发沿CD以![]() cm/s的速度移向点D移动,过E作直线EF∥BD交BC于F,再把△CEF沿着动直线EF对折,点C的对应点为点G. 若在整过移动过程中△EFG的直角顶点G能与点M重合.设运动时间为t(0<t≤3)秒.
cm/s的速度移向点D移动,过E作直线EF∥BD交BC于F,再把△CEF沿着动直线EF对折,点C的对应点为点G. 若在整过移动过程中△EFG的直角顶点G能与点M重合.设运动时间为t(0<t≤3)秒.
(1)求a的值;
(2)在运动过程中,
①当直线FG与⊙O相切时,求t的值;
②是否存在某一时刻t,使点G恰好落在⊙O上(异于点M)?若存在,请直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
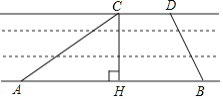
【题目】京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A、B和点C、D,先用卷尺量得AB=160m,CD=40m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com