练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．要了解下面的信息，适用普查的是（　　）
    A．深圳所有私家车每天的碳排放总量B．首届深圳国际马拉松的直播收视率
    C．全国中小学生的近视率D．校篮球队男队全体队员的平均身高

    分析 普查和抽样调查的选择．调查方式的选择需要将普查的局限性和抽样调查的必要性结合起来，具体问题具体分析，普查结果准确，所以在要求精确、难度相对不大，实验无破坏性的情况下应选择普查方式，当考查的对象很多或考查会给被调查对象带来损伤破坏，以及考查经费和时间都非常有限时，普查就受到限制，这时就应选择抽样调查．

    解答 解：A、深圳所有私家车每天的碳排放总量，应用抽样调查，故此选项错误；
    B、首届深圳国际马拉松的直播收视率，应用抽样调查，故此选项错误；
    C、全国中小学生的近视率，应用抽样调查，故此选项错误；
    D、校篮球队男队全体队员的平均身高，应采用全面调查方式，故此选项正确；
    故选：D．

    点评 此题考查了抽样调查和全面调查，由普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    17．运用公式计算：
    （1）（2$\sqrt{3}$+$\sqrt{6}$）（2$\sqrt{3}$-$\sqrt{6}$）；
    （2）（$\frac{3}{2}$$\sqrt{1\frac{2}{3}}$-$\sqrt{1\frac{1}{4}}$）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．河堤横断面如图所示，堤高BC=5m，迎水坡AB的坡比为1：2，则AC的长是10m．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．计算：4sin60°+$\sqrt{6}$÷$\sqrt{\frac{1}{2}}$-$\sqrt{\frac{9}{4}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．从2开始，连续的偶数相加，它们的和的情况如下表：当n个由2开始的连续偶数相加时，它们的和S与n之间有什么样的关系？用n的式子表示出来，并由此计算．
    加数的个数（n）和（S）
    12=1×2
    22+4=2×3
    32+4+6=12=3×4
    42+4+6+8=20=4×5
    52+6+6+8+10=30=5×6
    ……
    （1）若n=8时，则S的值为72；
    （2）根据表中的规律猜想：用n的式子表示S的公式为：S=2+4+6+6…+2n=n（n+1）；
    （3）根据（2）题的公式，计算：102+104+106+…+2012+2014．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．第1个等式：a1=$\frac{1}{1×3}=\frac{1}{2}×（1-\frac{1}{3}）$；第2个等式：a2=$\frac{1}{3×5}=\frac{1}{2}×（\frac{1}{3}-\frac{1}{5}）$；第3个等式：a3=$\frac{1}{5×7}=\frac{1}{2}×（\frac{1}{5}-\frac{1}{7}）$；第4个等式：a4=$\frac{1}{7×9}=\frac{1}{2}×（\frac{1}{7}-\frac{1}{9}）$；…
    解答下列问题：
    （1）按以上规律列出第5个等式，a5=$\frac{1}{9×11}$=$\frac{1}{2}$×（$\frac{1}{9}$-$\frac{1}{11}$）；
    （2）用含n的代数式第n个等式：an=$\frac{1}{（2n-1）（2n+1）}$=$\frac{1}{2}$×（$\frac{1}{2n-1}$-$\frac{1}{2n+1}$）（n为正整数）；
    （3）求a1+a2+a3+a4+…+a2014的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

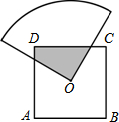    19．如图，O是边长为a的正方形ABCD的中心，将一块半径足够长，圆心为直角的扇形纸板的圆心放在O点处，并将纸板的圆心绕O旋转，求正方形ABCD的边被纸板覆盖部分的面积为（　　）
    A．$\frac{1}{2}{a^2}$B．$\frac{1}{3}{a^2}$C．$\frac{1}{4}{a^2}$D．无法计算

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

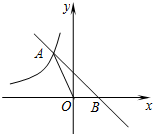    16．如图，直线y=-x+b与双曲线$y=-\frac{1}{x}$（x＜0）交于点A，与x轴交于点B，则OA2-OB2=（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．（1）知识再现
    如图（1）：若点A，B在直线l同侧，A，B到l的距离分别是3和2，AB=4，现在直线l上找一点P，使AP+BP的值最小，做法如下：
    作点A关于直线l的对称点A′，连接BA′，与直线l的交点就是所求的点P，线段BA′的长度即为AP+BP的最小值，请你求出这个最小值．
    （2）实践应用
    ①如图（2），⊙O的半径为2，点A、B、C在⊙O上，OA⊥OB，∠AOC=60°P是OB上一动点，则PA+PC的最小值是2$\sqrt{3}$
    ②如图（3），Rt△OAB的顶点A在x轴的正半轴上，顶点B的坐标为（3，$\sqrt{3}$），点C的坐标为（1，0），点P为斜边OB上的一动点，则PA+PC的最小值为$\sqrt{7}$
    ③如图（4），菱形ABCD中AB=2，∠A=120°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK的最小值为$\sqrt{3}$
    ④如图（5），在Rt△ABC中，∠C=90°，∠B=60°，点D是BC边上的点，CD=$\sqrt{3}$，将△ACD沿直线AD翻折，使点C落在AB边上的点E处，若点P是直线AD上的动点，则△PEB的周长的最小值是3+$\sqrt{3}$
    （3）拓展延伸
    如图（6）：在四边形ABCD的对角线AC上找一点P，使∠APB=∠APD，保留作图痕迹，不必写出作法．

    查看答案和解析>>

    同步练习册答案