
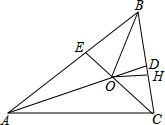
 已知:如图,在△ABC中,∠BAC、∠BCA的角平分线AD、CE相交于点O.OH⊥BC于点H,连接OB.
已知:如图,在△ABC中,∠BAC、∠BCA的角平分线AD、CE相交于点O.OH⊥BC于点H,连接OB.分析 (1)先判断点O为△ABC的内心,则利用内心性质得∠1=$\frac{1}{2}$∠ACB,∠2=$\frac{1}{2}$∠ABC,∠3=$\frac{1}{2}$∠BAC,再由三角形外角性质和三角形内角和定理可得∠BOD=90°-∠1,接着由OH⊥BC得到∠COH=90°-∠1,所以∠BOD=∠COH;
(2)作OQ⊥AC于Q,在AC上截取AG=AE=$\frac{14}{3}$,连结OG,如图,先在Rt△BOH中,利用含30度的直角三角形三边的关系得到OH=$\frac{1}{2}$OB=$\sqrt{3}$,再利用角平分线性质得OQ=OH=$\sqrt{3}$,接着证明△AEO≌△AGO得到△AOE=∠AOG=60°,所以∠COG=60°,然后证明△COG≌△COD得到CG=CD=$\frac{7}{3}$,所以AC=AG+CG=7,最后根据三角形面积公式求解.
解答 (1)证明:∵∠BAC、∠BCA的角平分线AD、CE相交于点O,
∴点O为△ABC的内心,
∴∠1=$\frac{1}{2}$∠ACB,∠2=$\frac{1}{2}$∠ABC,∠3=$\frac{1}{2}$∠BAC,
∴∠BOD=∠2+∠3
=$\frac{1}{2}$(∠ABC+∠BAC)
=$\frac{1}{2}$(180°-∠ACB)
=90°-∠1,
∵OH⊥BC,
∴∠COH=90°-∠1,
∴∠BOD=∠COH;
(2)解:作OQ⊥AC于Q,在AC上截取AG=AE=$\frac{14}{3}$,连结OG,如图,
在Rt△BOH中,∵∠OBH=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×60°=30°,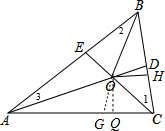
∴OH=$\frac{1}{2}$OB=$\frac{1}{2}$×2$\sqrt{3}$=$\sqrt{3}$,
∵OC平分∠ACB,
∴OQ=OH=$\sqrt{3}$,
∵点O为△ABC的内心,
∴∠AOC=90°+$\frac{1}{2}$∠ABC=120°,
∴∠AOE=60°,∠COD=60°,
在△AOE和△AOG中,
$\left\{\begin{array}{l}{AE=AG}\\{∠OAE=∠OAG}\\{AO=AO}\end{array}\right.$,
∴△AEO≌△AGO,
∴△AOE=∠AOG=60°,
∴∠COG=60°
在△COG和△COD中,
$\left\{\begin{array}{l}{∠COG=∠COD}\\{OC=OC}\\{∠OCG=∠OCD}\end{array}\right.$,
∴△COG≌△COD,
∴CG=CD=$\frac{7}{3}$,
∴AC=AG+CG=$\frac{14}{3}$+$\frac{7}{3}$=7,
∴S△AOC=$\frac{1}{2}$AC•OQ=$\frac{1}{2}$×7×$\sqrt{3}$=$\frac{7\sqrt{3}}{2}$.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.也考查了全等三角形的判定与性质和角平分线的性质.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
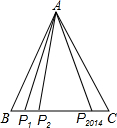 在△ABC中,AB=AC=1,BC边上有2014个不同的点P1,P2…,P2014,记mi=AP${\;}_{i}^{2}$+BPi•PiC(i=1,2,…,2014),求m1+m2+…+m2014的值.
在△ABC中,AB=AC=1,BC边上有2014个不同的点P1,P2…,P2014,记mi=AP${\;}_{i}^{2}$+BPi•PiC(i=1,2,…,2014),求m1+m2+…+m2014的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com